9. 动态规划（2）

动态规划（2）主要讲了动态规划的打家劫舍系列、买卖股票系列

198. 打家劫舍

198. 打家劫舍
0613，mid，quick
动态规划

方法一：二维dp

确定dp

dp[i][j] 表示偷窃到第 i 号房屋时的收益

dp[i][0] 表示不偷窃 i 号房屋
dp[i][1] 表示偷窃 i 号房屋

状态转移方程：

情况一：当前🏠 i 不偷，则上一个房屋偷也行，不偷也行，选择最大收益：Math.max(dp[i - 1][1], dp[i - 1][0])。
情况二：当前🏠 i 偷：则只能是上一个房屋不偷 => dp[i - 1][0] + nums[i]。

初始化
遍历

var rob = function (nums) {
  // dp[i][j] 表示偷窃到第i号房屋时的收益
  // dp[i][0] 表示不偷窃i号房屋
  // dp[i][1] 表示偷窃i号房屋。
  const dp = Array.from(new Array(nums.length), () => new Array(2).fill(0));
  dp[0][1] = nums[0];

  for (let i = 1; i < nums.length; i++) {
    // i不偷：前一天偷/不偷的最大收益
    dp[i][0] = Math.max(dp[i - 1][1], dp[i - 1][0]);
    // i偷：[i-1] 没偷，则i能偷
    dp[i][1] = dp[i - 1][0] + nums[i];
  }
  // console.log(dp);
  return Math.max(dp[nums.length - 1][0], dp[nums.length - 1][1]);
};

方法二：一维dp

确定dp

dp[i]：i（包括i）以内的房屋，最多可以偷窃的金额为dp[i]

状态转移方程

有两种情况，第 i 房间偷还是不偷：

偷第 i 房间，那么 dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定不能偷，最多偷窃的金额为 dp[i-2] + 第 i 房间偷的钱。
不偷第 i 房间，那么dp[i] = dp[i - 1]，即：考虑 i-1 房可以偷，收益是 i-1房的最大收益（不一定偷了 i - 1）。

最后，取最大值，即 dp[i] = max(dp[i - 2] + nums[i], dp[i - 1])；

初始化

dp[0] 一定是偷，才有最大收益 nums[0]，不偷的收益是 0；

0 dp[1] 如果不偷，收益是 nums[0]；如果偷，收益是 num[1]。取最大值。

var rob = function (nums) {
  const dp = [];
  dp[0] = nums[0];
  dp[1] = Math.max(nums[0], nums[1]);

  for (let i = 2; i < nums.length; i++) {
    // 不偷 + 偷
    dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
  }
  // console.log(dp);
  return dp[nums.length - 1];
};

方法三：一维dp｜滚动数组

因为 dp[i] 只被 i-1 和i-2 影响，所以设置一个长度为 2 的 dp 即可。

注意：因为 return 的 dp 从 dp[length - 1] 修改为固定的 dp[1]，所以注意 nums 长度为 1 的情况。在开头判断特例。

var rob = function (nums) {
  if (nums.length === 1) return nums[0];
  const dp = [nums[0], Math.max(nums[0], nums[1])];

  for (let i = 2; i < nums.length; i++) {
    const profit = Math.max(dp[1], dp[0] + nums[i]); // 不偷 + 偷
    [dp[0], dp[1]] = [dp[1], profit];
  }
  return dp[1];
};

213. 打家劫舍 II

213. 打家劫舍 II
0613，mid，answer
动态规划

方法一：一维dp

根据分析题意，可以拆分出两种情况：

如果🏠 1 偷窃了，最后一个房屋就不能偷窃，判断偷窃的房屋范围是：[0, len - 1]；
如果🏠 1 不偷窃，最后一个房屋就不受影响，正常可偷。判断偷窃的房屋范围是：[1, len]；

则定制个方法 robbing，入参 start，len。用来表示遍历的房屋范围。

最后结果返回两个 case 的较大值。

var rob = function (nums) {
  // 特例：
  if (nums.length === 1) return nums[0];
  // 情况一：如果第一个被偷，最后一个不能偷，前一个可以偷，房屋范围：[0, len - 1]
  const case1 = robbing(0, nums.length - 1);
  // 情况二：如果第一个没偷，最后一个可以偷，房屋范围：[1, len - 2]
  const case2 = robbing(1, nums.length);
  return Math.max(case1, case2);

  function robbing(start, len) {
    // 在[start, len]这个范围内偷窃，而不是之前的[0, len]
    const dp = [];
    // 初始化
    dp[start] = nums[start];
    dp[start + 1] = Math.max(nums[start], nums[start + 1]);

    for (let i = start + 2; i < len; i++) {
      dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]); // 不偷 + 偷
    }
    return dp[len - 1];
  }
};

方法二：一维dp｜滚动数组

这道题当然也可以用滚动数组，对 robbing 稍加改动即可：

注意特例要对 nums.length === 2 时判断。

var rob = function (nums) {
  // 特例：
  if (nums.length === 1) return nums[0];
  if (nums.length === 2) return Math.max(nums[0], nums[1]);
  // 情况一：如果第一个被偷，最后一个不能偷，房屋范围：[0, len - 1]
  const case1 = robbing(0, nums.length - 1);
  // 情况二：如果第一个没偷，最后一个可以偷，房屋范围：[1, len - 2]
  const case2 = robbing(1, nums.length);
  return Math.max(case1, case2);

  function robbing(start, len) {
    const dp = [nums[start], Math.max(nums[start], nums[start + 1])];

    for (let i = start + 2; i < len; i++) {
      const profit = Math.max(dp[1], dp[0] + nums[i]); // 不偷 + 偷
      dp[0] = dp[1];
      dp[1] = profit;
    }
    return dp[1];
  }
};

337. 打家劫舍 III

337. 打家劫舍 III
0613，mid，
记忆化递归，动态规划

树的递归，是自下而上去做统计的。

比如判断某个节点 A 的最大收益，是判断 A 已经连带它的孩子、孙子 ... 的最大收益，所以：

叶子结点的最大收益就是自身 node.val；
空节点没有收益，收益值为 0；

这和传统的 dp 从前往后叠加收益不同，是从底向上叠加收益。

方法一：记忆化递归

对二叉树考虑 dfs 递归。

使用后序遍历。通过递归函数的返回值来做下一步计算。即：先获得了左右孩子的值，自身的值才能确定。

状态转移方程：

当遍历到某个节点时，有两个 case：

case1：偷当前节点的房子，则收益为：当前房屋的收益 + 左右孩子各自孩子的收益（跳过左右两个孩子，看四个孙子）；
case2：不偷当前节点的房子，则收益为：左右孩子的收益（跳过自身收益，看两个孩子）；

最后当前节点的最佳收益：Math.max(case1, case2)。

记忆化递归：用 map 结构来存储每个节点计算的收益，防止重复计算。

为什么会重复计算？
因为这不是传统的先序、中序、后序遍历。
遍历道当前节点时，我们会直接遍历其 2 个孩子节点 + 4 个孙子节点；而遍历到左孩子节点时，也会遍历它的两个孩子，也就是当前节点的孙子节点，这就发生了重复。

var rob = function (root) {
  const map = new Map();
  return dfs(root);

  //  表达当前node节点返回的收益
  function dfs(node) {
    if (node === null) return 0 // 遍历到头，没有节点了，返回收益0
    if (map.has(node)) return map.get(node); // 如果map已经保存该值，则直接返回
    // 偷自身，跳过左右子节点，直接获得左右孩子的孩子返回的收益
    let profit1 = node.val;
    if (node.left) profit1 += dfs(node.left.left) + dfs(node.left.right);
    if (node.right) profit1 += dfs(node.right.left) + dfs(node.right.right);
    // 偷子节点，跳过自身，获得左右孩子返回的收益
    let profit2 = dfs(node.left) + dfs(node.right);
    map.set(node, Math.max(profit1, profit2));
    return map.get(node);
  }
};

方法二：动态规划

相比记忆化递归的好处：

避免重复计算节点。因为动态规划思想的递归，并没有跳过任何一个节点，而是完全正常的按序后序遍历。

为什么可以不用跳过？
因为每次递归的返回值都是两种情况：偷和不偷。所以当前节点拿到孩子节点的返回值，根据自己 case 的要求，获取相应的数值就可以。
- 比如在记忆化递归中，如果当前节点选择不偷，那么要跳过孩子，获取四个孙子的最大收益。
- 而在动态规划中，如果当前当前节点选择不偷，不需要跳过，直接选择孩子节点中不偷的结构即可 dp[0]。

思路：

对树结构的动态规划，要结合二叉树 + 动态规划的解题方法：

递归三部曲：确定递归函数（入参 / 出参）、确定终止条件、确定遍历顺序
动归五部曲：确定 dp 含义、确定状态转移方程、确定 dp 初始化、确定遍历条件、手动dp一个案例验证

确定：递归函数（入参 / 出参）+ dp 含义

对每个节点（房屋）有偷 / 不偷两个 case，则递归返回值应当是一个长度为 2 的数组：[偷，不偷]，分别是偷和不偷的最大收益。

dp[0]：当前节点不偷的最大收益；
dp[1]：当前节点偷的最大收益。

这其实是一个二维 dp，调用栈中的每个函数都会生成一个长度为 2 的数组。这相当于 dp[i][0] 和 dp[i][1]。

确定终止条件

遇到空节点则达到边界，返回 0。

if (node == NULL) return [0, 0];

确定遍历顺序

后序遍历。通过递归函数的返回值来做下一步计算。

左、右、根

状态转移方程

// 后序遍历：获取左右节点偷/不偷的收益
const left = dfs(node.left);
const right = dfs(node.right);
const val = node.val;
// 不偷当前节点：左右孩子都能偷，分别取他们的较大值
const profit1 = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
// 偷当前节点：val
const profit2 = val + left[0] + right[0];
return [profit1, profit2];

得代码：

var rob = function (root) {
  const [profit1, profit2] = dfs(root);
  return Math.max(profit1, profit2);

  // 表达当前node节点返回的收益
  function dfs(node) {
    if (node === null) return [0, 0];
    // 后序遍历：获取左右节点偷/不偷的收益
    const left = dfs(node.left);
    const right = dfs(node.right);
    const val = node.val;
    // 不偷当前节点：左右孩子都能偷，分别取他们的较大值
    const profit1 = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
    // 偷当前节点：val
    const profit2 = val + left[0] + right[0];
    return [profit1, profit2];
  }
};

股票问题总结

121. 买卖股票的最佳时机

121. 买卖股票的最佳时机
0613，easy，normal

方法一：贪心

结果为：右侧最大值 - 左侧最小值。最大值的下标应比最小值的下标靠右。

low 一直获取更靠左侧的最小值；
result 不断计算当前值 - 当前最小值的收益。

var maxProfit = function (prices) {
  // 贪心：获取最小值和最大值
  let result = 0;
  let low = prices[0];
  for (let i = 0; i < prices.length; i++) {
    low = Math.min(prices[i], low);
    result = Math.max(result, prices[i] - low);
  }
  return result;
};

方法二：动态规划｜滚动数组

用二维 dp[i][j] 记录：

dp[i][0]：当前 i 价格不持有股票；
dp[i][1]：当前 i 价格持有股票；

注意状态转移方程：

不持有：如果前一天不持有，就保持不变；如果前一天持有，就当前卖出，获得收益。
- Math.max(dp[0], dp[1] + prices[i]);
持有：如果一直不持有，则当前 第一次 当前买入；如果前一天持有，则保持不变
- Math.max(-prices[i], dp[1]);
- 注意：这里一定是第一次买入，因为题目中要求只能有一次买入，所以如果在当前价格买入，那收益一定是 -prices[i]，之前一定没有进行过任何交易。

这里直接把二维数组优化为长度为 2 的滚动数组：

var maxProfit = function (prices) {
  // 当前i价格：dp[i][0]不持有股票, dp[i][1]持有股票
  const dp = [0, -prices[0]];
  for (let i = 1; i < prices.length; i++) {
    // 不持有:前一天不持有,保持不变 + 前一天持有,当前卖出,获得收益
    const unhold = Math.max(dp[0], dp[1] + prices[i]);
    // 持有:一直不持有,当前买入 + 前一天持有,保持不变
    const hold = Math.max(-prices[i], dp[1]);
    dp[0] = unhold;
    dp[1] = hold;
  }
  return dp[0];
};

122. 买卖股票的最佳时机 II

122. 买卖股票的最佳时机 II
0613，mid，quick
动态规划

方法一：动态规划｜滚动数组

如果想看传统的二维dp解析，见：贪心章节中对该题的解答。

与上一题相比，可以多次买卖，每次是否持有发生改变，都需要参考上一次（dp[i-1]）的值。

这里直接把二维数组优化为长度为 2 的滚动数组：

var maxProfit = function (prices) {
  // dp[i][0] 表示第i天不持有
  // dp[i][1] 表示第i天持有
  const dp = [0, -prices[0]];
  for (let i = 0; i < prices.length; i++) {
    // 不持有：之前不持有；之前持有，卖出
    const unhold = Math.max(dp[0], dp[1] + prices[i]);
    // 持有：之前不持有，买入；之前持有
    const hold = Math.max(dp[0] - prices[i], dp[1]);
    dp[0] = unhold;
    dp[1] = hold;
  }
  return dp[0];
};

123. 买卖股票的最佳时机 III

123. 买卖股票的最佳时机 III
0613，hard，answer
动态规划

本题可最多交易2次，这意味着可以有 1～2 次交易，先从状态机角度分析这五种状态：

没有任何买入 / 卖出行为，状态一：不持有股票：dp[i][0]
第一次买入 ===> 状态二，持有第一支股票：dp[i][1]
第一次卖出 ===> 状态三，不持有股票：dp[i][2]
第二次买入 ===> 状态四，持有第二支股票：dp[i][3]
第二次卖出 ===> 状态五，不持有股票：dp[i][4]

定义 dp

所以，从上面顺便也定义了 dp 的含义：dp[i][j] 表示当股票价格为 i 时的状态。

初始化：

dp[0][0] 没有任何交易，一定为 0；
dp[0][1] 购入第一支股票，收益为 -prices[i]
dp[0][2] 出售第一支股票，可以想象为当天买当天卖，收益 0；
dp[0][3] 购入第二支股票，想象为当天买卖了第一支，收益 0 ，买入第二支收益为 -prices[i]
dp[0][4] 出售第二支股票，当天买的当天卖，收益 0。

var maxProfit = function (prices) {
  const dp = Array.from(new Array(prices.length), () => new Array(5).fill(0));
  dp[0][1] = -prices[0];
  dp[0][3] = -prices[0];

  for (let i = 1; i < prices.length; i++) {
    // 没有买卖
    dp[i][0] = dp[i - 1][0];
    // 持有第一支股票:以前持有 + 刚持有
    dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
    // 已出售第一支股票:以前出售 + 刚出售
    dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
    // 持有第二支
    dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
    // 已出售第二支
    dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
  }
  return dp[prices.length-1][4];
};

方法二：一维dp｜滚动数组

当前时间 i 的收益只受上一个时间 i - 1的影响，所以可以优化为滚动数组。
同时可以省略情况一，因为最开始没有买卖，收益一定是一直为 0 的。

var maxProfit = function (prices) {
  let dp = new Array(4).fill(0);
  dp[0] = -prices[0];
  dp[2] = -prices[0];

  for (let i = 1; i < prices.length; i++) {
    // 持有第一支股票:以前持有 + 刚持有
    const r0 = Math.max(dp[0], -prices[i]);
    // 已出售第一支股票:以前出售 + 刚出售
    const r1 = Math.max(dp[1], dp[0] + prices[i]);
    // 持有第二支
    const r2 = Math.max(dp[2], dp[1] - prices[i]);
    // 已出售第二支
    const r3 = Math.max(dp[3], dp[2] + prices[i]);
    dp = [r0, r1, r2, r3];
  }
  return dp[3];
};

188. 买卖股票的最佳时机 IV

188. 买卖股票的最佳时机 IV
0614，hard，quick
动态规划

方法一：二维dp数组

思路其实就是（123. 买卖股票的最佳时机 III）的延伸：

如果是两次交易 dp[i][j] 中，j 的长度就是 5；
如果是 k 次交易，那 j 的长度就是 2 * k + 1；

倒序：

因为 dp[j] 受到 dp[j-1] 的影响，所以如果 j 从前往后遍历，就会影响到前一位的 dp[j-1] ，那么 j 从后往前遍历并更新值即可。

var maxProfit = function (k, prices) {
  if (prices.length <= 1) return 0;
  let dp = new Array(k * 2 + 1).fill(0);

  // 第0次不买不卖，奇数持有，偶数不持有
  for (let i = 1; i <= k * 2; i++)
    if (i % 2) dp[i] = -prices[0];

  for (let i = 1; i < prices.length; i++) {
    for (let j = k * 2; j >= 1 ; j--) { // 倒序
      dp[j] = j % 2
        ? Math.max(dp[j], dp[j - 1] - prices[i])  // 第x次持有：以前持有 + 刚买入
        : Math.max(dp[j], dp[j - 1] + prices[i])  // 第x次不持有：以前不持有 + 刚卖出
    }
  }
  return dp[k * 2];
};

方法二：一维dp数组

var maxProfit = function (k, prices) {
  if (prices.length <= 1) return 0;

  let dp = new Array(k * 2 + 1).fill(0);

  // 第0次不买不卖，奇数持有，偶数不持有
  for (let i = 1; i <= k * 2; i++)
    if (i % 2) dp[i] = -prices[0];

  for (let i = 1; i < prices.length; i++) {
    const newdp = new Array(k * 2 + 1).fill(0);
    for (let j = 1; j <= k * 2; j++) {
      newdp[j] = j % 2
        ? Math.max(dp[j], dp[j - 1] - prices[i])  // 第x次持有：以前持有 + 刚买入
        : Math.max(dp[j], dp[j - 1] + prices[i])  // 第x次不持有：以前不持有 + 刚卖出
    }
    dp = [...newdp];
  }
  return dp[k * 2];
};

309. 最佳买卖股票时机含冷冻期

309. 最佳买卖股票时机含冷冻期
0614，mid，answer
动态规划

思路：重点是要把这几个状态分析清楚，要把冷冻期考虑在状态转移的类型内。

状态转移方程

case1：持有股票（一直持有 / 刚买入(前一天是冷冻期，前一天已经过了冷冻期)）；
case2：一直不持有股票，过了冷冻期(保持不变，前一天是冷冻期)
case4：刚不持有股票，卖出
case3：不持有股票，前一天刚卖出，还在冷冻期；

初始化：

case1：持有股票，最开始刚持有股票，收益肯定是 -prices[0]；

不持有股票，收益最低也只能为 0，不可能为负数：

case2：一直不持有股票，收益为 0；
case4：刚不持有股票，收益为 0；
case3：不持有股票，前一天刚卖出，还在冷冻期：收益为 0.

解题：

var maxProfit = function (prices) {
  if (prices.length <= 1) return 0

  const dp = Array.from(new Array(prices.length), () => new Array(4).fill(0));
  dp[0][0] = -prices[0];

  for (let i = 1; i < prices.length; i++) {
    // case1：持有股票（一直持有 / 刚买入(前一天是冷冻期，前一天已经过了冷冻期)）；
    dp[i][0] = Math.max(dp[i - 1][0], Math.max(dp[i - 1][1], dp[i - 1][3]) - prices[i]);
    // case2：一直不持有股票，过了冷冻期(保持不变，前一天是冷冻期)
    dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][3]);
    // case3：刚不持有股票，卖出
    dp[i][2] = dp[i - 1][0] + prices[i];
    // case4：不持有股票，前一天刚卖出，还在冷冻期；
    dp[i][3] = dp[i - 1][2];
  }
  return Math.max(dp[prices.length - 1][1], dp[prices.length - 1][2], dp[prices.length - 1][3]);
};

714. 买卖股票的最佳时机含手续费

与普通的买卖股票相比，就是在出售的时候多剪掉一个手续费即可：

var maxProfit = function (prices, fee) {
  const dp = [0, -prices[0]];  // 不持有，持有

  for (let i = 1; i < prices.length; i++) {
    // 不持有:(保持不持有，刚卖)
    sell = Math.max(dp[0], dp[1] + prices[i] - fee);
    // 持有:(保持持有，刚买)
    buy = Math.max(dp[1], dp[0] - prices[i]);
    dp[0] = sell;
    dp[1] = buy;
  }
  return dp[0];
};

300. 最长递增子序列

300. 最长递增子序列
0614，mid，answer
动态规划

时间复杂度：O(nlgn)

dp[i] 表示在下标 [0, i] 区间内，最长递增子序列的长度为多少。

状态转移方程：

[0, i] 之间是否存在 j，它的值 nums[j] 是小于 nums[i] 的。通过 for 循环找到所有比 nums[i] 小的值。然后获得他们的最长递增子序列长度 dp[j] 。则 dp[i] 的值就是全部这些 dp[j] 中最大的一个，再加1；

res 用来统计最终的结果，每次 for 循环过后都更新 res 为 dp 中的最大值，省去 return 的时候判断最大值。

初始化：

子序列最短也一定为 1，所以 res 和 dp 成员的默认值为最小的 1，不要设置为 0。

var lengthOfLIS = function (nums) {
  //  dp[i] 到数字i时，最长的子序列
  const dp = new Array(nums.length).fill(1);
  let res = 1;
  for (let i = 1; i < nums.length; i++) {
    for (let j = 0; j < i; j++) {
      if (nums[j] < nums[i]) dp[i] = Math.max(dp[i], dp[j] + 1);
      res = Math.max(res, dp[i]);
    }
  }
  // console.log(dp);
  return res;
};

674. 最长连续递增序列

674. 最长连续递增序列
0614，easy，quick
动态规划

方法一：一维dp

状态转移方程：如果当前值 nums[i] 大于上一个 nums[i - 1]，那么总数就是 dp[i - 1] + 1，否则就重新计算，值为 1。

var findLengthOfLCIS = function (nums) {
  const dp = Array(nums.length).fill(1);
  let res = 1;

  for (let i = 1; i < nums.length; i++) {
    if (nums[i - 1] < nums[i]) dp[i] = dp[i - 1] + 1;
    res = Math.max(res, dp[i]);
  }
  return res;
};

方法二：滚动数组

因为 dp[i] 只依赖于前一个值 dp[i-1]，所以只保存当前值为 point 即可，不断更新 point 的值。res 用来统计 point 曾经的最大值。

var findLengthOfLCIS = function (nums) {
  let point = res = 1;

  for (let i = 1; i < nums.length; i++) {
    point = nums[i - 1] < nums[i] ? point + 1 : 1;
    res = Math.max(res, point);
  }
  return res;
};

718. 最长重复子数组

718. 最长重复子数组
0614，mid，answer
动态规划

为什么没做出来？这两个没考虑清楚：

两个数组的每个元素各自进行对比，对比后有一个结果（是否相等）。这个结果要进行记录，一定是用二维 dp。
数组 A 和数组 B 的中有两个元素 i ，j，一旦相等，那此时的最长重复字数组长度就应当是 i-1，i-1 长度 + 1。

方法一：二维dp

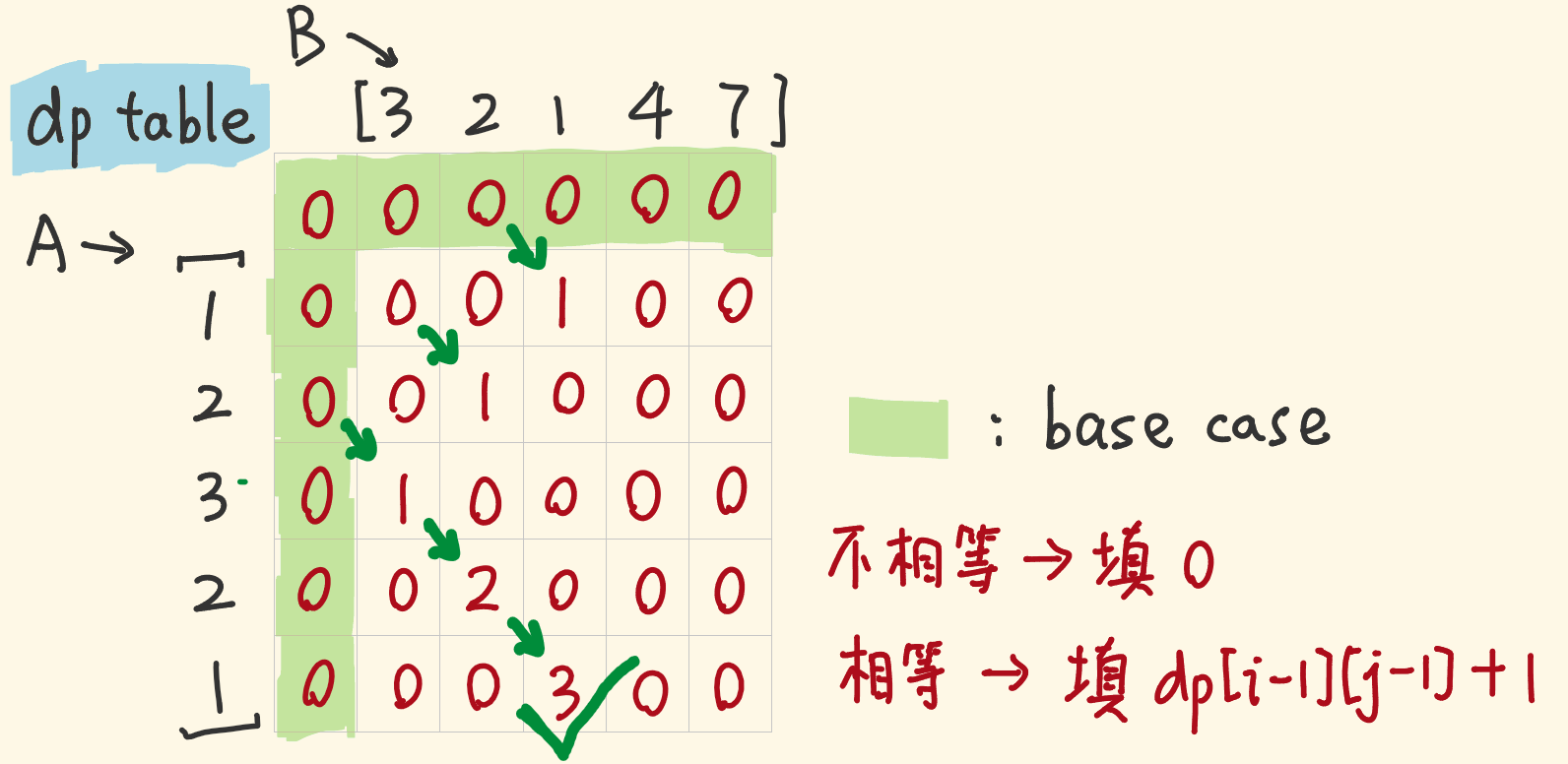
9b80364c7936ad0fdca0e9405025b2a207a10322e16872a6cb68eb163dee25ee-image

定义 dp

dp[i][j] ：数组 A [0, i-1] 区间，数组 B [0, j-1] 区间的最长重复子数组长度

为什么是 i-1? 因为二维数组的左边 dp[x][0]和上边 dp[0][x]，定义为没有实际意义的空位置，赋默认值为 0（上图）。这样才能确保状态转移方程正确。

确定状态转移方程

要把 [1,i-1] 的 A 数组，和 [1,j-1] 的 B 数组内每个成员都要比较一次。

如果遇到值相等，则 dp[i][j] = dp[i - 1][j - 1] + 1

初始化

因为区间是从 [0, i-1] 开始判断，则从 1 开始判断，dp[0][0]、dp[0][x]、dp[x][0] 都没有意义，设置为 0；

var findLength = function (nums1, nums2) {
  const dp = Array.from(new Array(nums1.length + 1), () => new Array(nums2.length + 1).fill(0));
  let res = 0;

  for (let i = 1; i <= nums1.length; i++) {
    for (let j = 1; j <= nums2.length; j++) {
      if (nums1[i - 1] === nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
      res = Math.max(res, dp[i][j]);
    }
  }
    return res;
};

方法二：一维dp

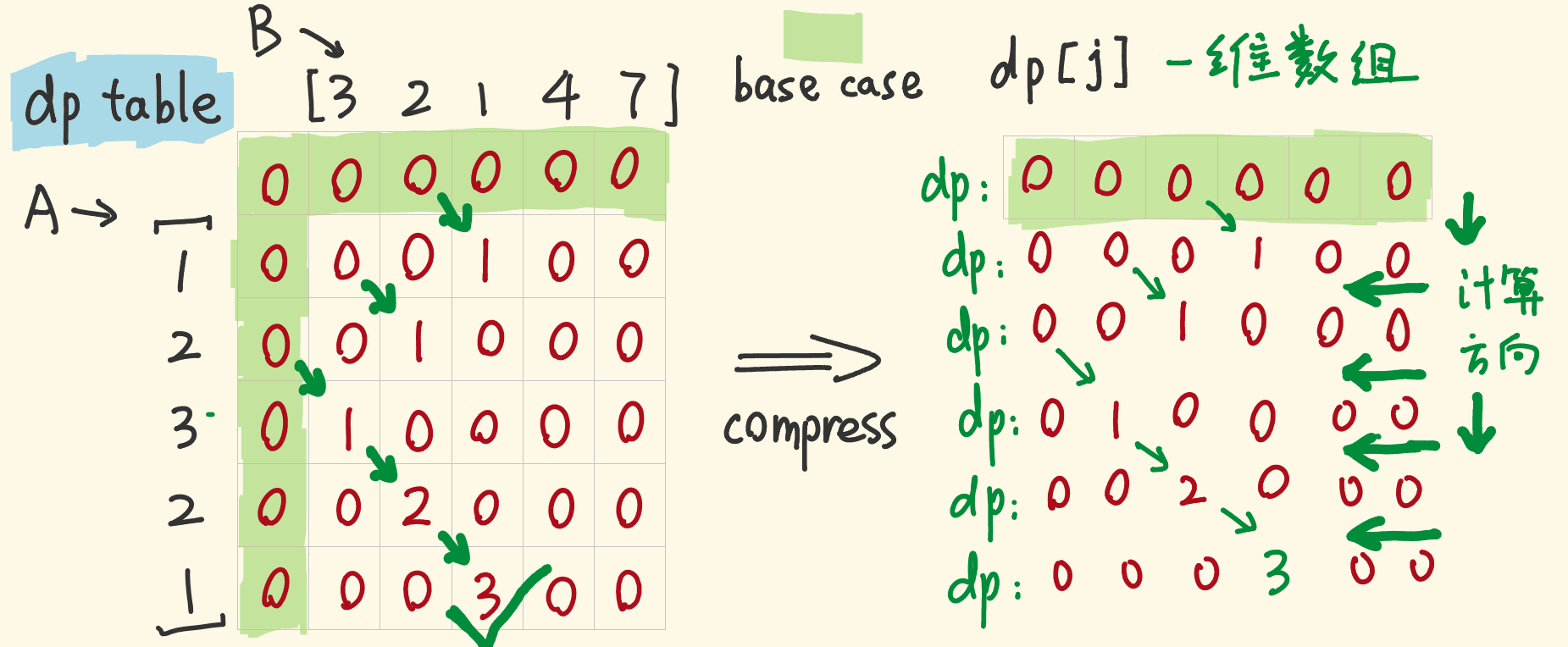
1058100aea8006ae91abbad52076aae5f3782d7562d21dff55b8010744f8f511-image

倒序：

因为 dp[j] 受到 dp[j-1] 的影响，所以如果 j 从前往后遍历，就会影响到前一位的 dp[j-1] ，那么 j 从后往前遍历并更新值即可。

注意，因为 dp 数组是一维的被复用，所以初始值 0 有可能在上一轮的时候已经设置为新的值，这时在状态转移方程是重新设置为 0

var findLength = function (nums1, nums2) {
  let dp = new Array(nums2.length + 1).fill(0);
  let res = 0;

  for (let i = 1; i <= nums1.length; i++) {
    for (let j = nums2.length; j >= 1; j--) {
      dp[j] = nums1[i - 1] === nums2[j - 1]
        ? dp[j - 1] + 1
        : 0 // 默认值要重新设置为 0
      res = Math.max(res, dp[j]);
    }
  }
  return res;
};

1143.最长公共子序列

1143. 最长公共子序列
0614，mid，answer
动态规划

定义 dp

dp[i][j]：长度为 [0, i - 1] 的字符串 text1 与长度为 [0, j - 1] 的字符串 text2 的最长公共子序列为 dp[i][j]。

定义状态转移方程

注意：因为是判断 [0, i - 1] 和 [0, j - 1] 这个区间，所以当前判断点位应当是 i - 1 和 j - 1。

case1：text1[i - 1] 与 text2[j - 1] 相同

找到了一个公共元素，所以 text1 和 text2 都前进一位，dp[i][j] = dp[i - 1][j - 1] + 1;

case2：text1[i - 1] 与 text2[j - 1]不相同

则让 text1 或 text2 其中一个前进一位，谁的最长公共子序列更长，就选谁的结果：dp[i][jmax(dp[i - 1][j], dp[i][j - 1])

有三个方向可以递推出 dp[i][j]：

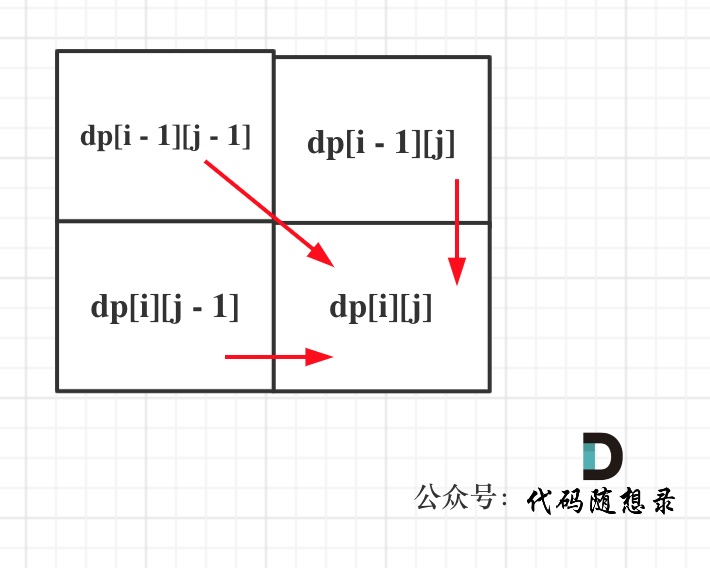
20210204115139616

代码：

var longestCommonSubsequence = function (text1, text2) {
  const dp = Array.from(new Array(text1.length + 1), () => new Array(text2.length + 1).fill(0));

  for (let i = 1; i <= text1.length; i++) {
    for (let j = 1; j <= text2.length; j++) {
      dp[i][j] = text1[i - 1] === text2[j - 1]
        ? dp[i - 1][j - 1] + 1
        : Math.max(dp[i - 1][j], dp[i][j - 1])
    }
  }
  return dp[text1.length][text2.length];
};

1035. 不相交的线

1035. 不相交的线
0614，mid，answer
动态规划

本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度

要剖析题干要求，找到规律。nums1 和 nums2 两个数组中，最终被连线的字母所组成的子序列，一定是完全相等的。

20210914145158

代码与（1143.）一模一样。

var maxUncrossedLines = function (nums1, nums2) {
  const dp = Array.from(new Array(nums1.length + 1), () => new Array(nums2.length + 1).fill(0));

  for (let i = 1; i <= nums1.length; i++) {
    for (let j = 1; j <= nums2.length; j++) {
      dp[i][j] = nums1[i - 1] === nums2[j - 1]
        ? dp[i - 1][j - 1] + 1
        : Math.max(dp[i - 1][j], dp[i][j - 1])
    }
  }
  return dp[nums1.length][nums2.length];
};

53. 最大子数组和

53. 最大子数组和
0614，easy，quick
贪心，动态规划

方法一：贪心

注意点一：cur 记录遍历时实时统计的总和，res 记录所有 cur 中的最高值

注意点二：如果 cur 已经小于 0 了，那就直接放弃之前统计的数字，从 0 开始；反之，就把当前值加到 cur 上。

var maxSubArray = function (nums) {
  // 贪心
  let cur = -Infinity;
  let res = -Infinity;
  for (let i = 0; i < nums.length; i++) {
    if (cur < 0) cur = Math.max(cur + nums[i], nums[i]);
    else cur += nums[i];
    res = Math.max(cur, res);
  }
  return res;
};

方法二：动态规划

可以看到，贪心就是动态规划的一维 dp 思路。

dp[i] 的状态转移方程：
- case1：继续累加和
- case2：不再累加，而是从 0 开始。

dp[i] 记录两者的较大值。

初始化

注意初始化，dp[0] 和 res 应当为 nums[0]。

var maxSubArray = function (nums) {
  const dp = new Array(nums.length).fill(-Infinity);
  dp[0] = nums[0];
  let res = nums[0];
  for (let i = 1; i < nums.length; i++) {
    dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
    res = Math.max(res, dp[i]);
  }
  return res;
};

392. 判断子序列

392. 判断子序列
0614，easy，normal
动态规划

方法一：动态规划

问题转化为：判断 s 是否是 t 的子序列，就是要在 t 中能否按需查找到一个 s。

定义 dp

dp[i][j] 表示，从区间为 [0, j-1] 的字符串 t，寻找区间为 [0, i-1] 的字符串 s ，能找到的最长长度。

定义状态转移方程

case1：s[i-1] === t[j-1] ，也就是当前判断的两个数字相等，则统计数字可以 + 1：dp[i][j] = dp[i-1][j-1] + 1。
case2：s[i-1] !== t[j-1] ，
- 题目的目的是把 s 全部匹配掉，所以 s 的每一个成员是不可跳过的。
- 当 i -1 这个元素没有匹配上时，就继续等待 i -1，跳过 j -1。这相当于 t 要删除元素 t[j - 1]，那么 dp[i][j] 的数值就是看 s[i - 1]与 t[j - 2] 的比较结果了：dp[i][j] = dp[i][j - 1]。

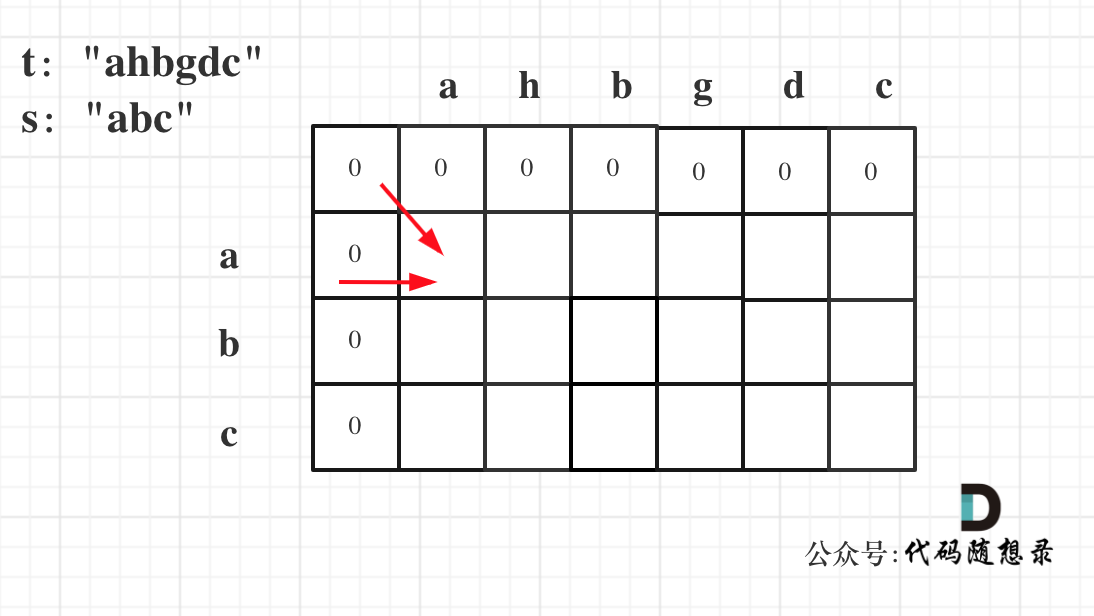
20210303173115966

var isSubsequence = function (s, t) {
  const dp = Array.from(new Array(s.length + 1), () => new Array(t.length + 1).fill(0));

  for (let i = 1; i <= s.length; i++) {
    for (let j = 1; j <= t.length; j++) {
      dp[i][j] = s[i - 1] === t[j - 1]
        ? dp[i - 1][j - 1] + 1
        : dp[i][j - 1]
    }
  }
  return dp[s.length][t.length] === s.length
};

方法二：双指针

两个指针分别指向两个数组，如果相当则子序列指针 +1。

var isSubsequence = function (s, t) {
  let sp = 0; // 子序列
  let tp = 0;

  while (sp < s.length && tp < t.length) {
    if (s[sp] === t[tp]) sp++
    tp++;
  }
  return sp === s.length;
};

115. 不同的子序列

115. 不同的子序列
hard，跳过，answer
递归、动态规划

翻译题意

读懂题目后，用自己的话“翻译”一下题目，有时候会更容易有思路。

题目：求 s 的子序列中 t 出现的个数，blabla...
翻译：在 s 串身上 “挑选” 字符，去匹配 t 串的字符，求挑选的方式数

从后往前：从最终得到的结果开始，一步一步往前推，直到算出初始的结果后，就可以得出最终的结果，即递归的方法。

从前往后：从最开始最优的一步，一直往最终的结果推，直到推出最终的结果，这是动态规划的方法。

方法一：dfs 递归

思路：

抓住 “选”，s 要照着 t 来挑选，逐个字符判断选 / 不选，分别下一个状态是什么？

举例，s 为 babgbag，t 为 bag，末尾字符相同，于是 s 有两种选择：

用 s[s.length-1] 去匹配掉 t[t.length-1] ，问题规模缩小：继续考察 babgba 和 ba；
不这么做，但 t[t.length-1] 仍需被匹配，于是在 babgba 中继续挑，考察 babgba 和 bag

是否用 s 的当前字符去匹配，是两种不同的挑选方式，各自分支下去所统计的方式数，相加，是大问题的解。

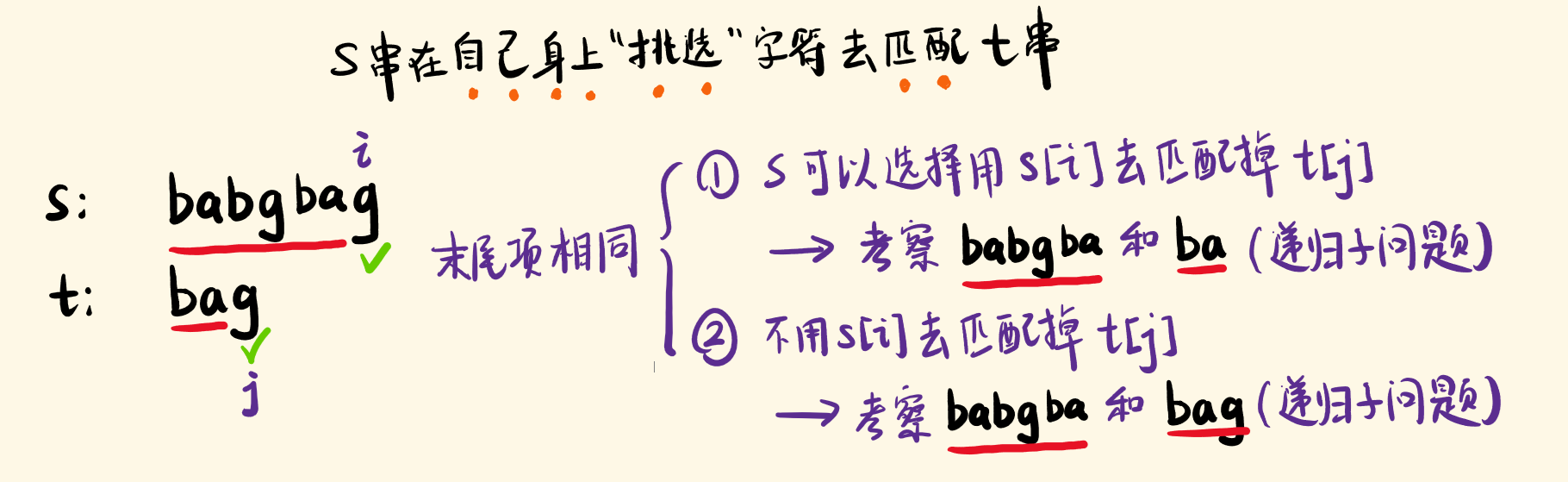
1615916797-rXJnAT-image

现在我们拆解出规模小一点的子问题。完善一下，定义出递归函数：

返回：从开头到 s[i] 的子串中，出现『从开头到 t[j] 的子串』的次数。即，从前者选字符，去匹配后者的方案数。

看了 s[i]===t[j] 的情况，那 s[i]!==t[j] 的情况呢？s[i] 不匹配 t[j]，唯有拿 s[i] 之前的子串去匹配。

现在两种情况下的递归公式都好写了。递归树底部的 base case 呢？

随着递归压栈，子问题规模（子串长度）在变小：

小到 t 变成空串，此时 s 为了匹配它，方式只有1种：什么字符也不用挑（或 s 也是空串，什么都不做就匹配了，方式数也是1）
小到 s 变成空串，但 t 不是，s 怎么也匹配不了 t，方式数为 0

var numDistinct = function (s, t) {
  return helper(s.length - 1, t.length - 1);

  // i 长串、j 短串
  function helper(i, j) {
    if (j < 0) return 1;
    if (i < 0) return 0;

    return s[i] === t[j]
      ? helper(i - 1, j) + helper(i - 1, j - 1)
      : helper(i - 1, j)
  }
};

从头开始递归也更好理解：

var numDistinct = function (s, t) {
  return dfs(0, 0);

  function dfs(longer, smaller) {
    if (smaller === t.length) return 1;
    if (longer === s.length) return 0;

    return t[smaller] === s[longer]
      ? dfs(longer + 1, smaller) + dfs(longer + 1, smaller + 1)
      : dfs(longer + 1, smaller);
  }
};

结果超时，需要记忆化搜索。

方法二：递归｜记忆化搜索

上面的题解中有许多重复的计算，比如给 helper(i - 1, j) + helper(i - 1, j - 1) 模拟赋值：i = 3，j = 3

helper(2, 3) + helper(2, 2) ，这样递归下去
- 左侧的 helper 可能会计算：helper(1,3) 、helper(1,2)
- 右侧的 helper 可能会计算：helper(1,2) 、helper(1,1)

可以看到，这里面已经重复计算了，那么我们需要一个 memo，去统计已经计算的结果。memo 设置为一个二维数组：

var numDistinct = function (s, t) {
  const memo = Array.from(new Array(s.length), () => new Array(t.length).fill(Infinity));
  return helper(s.length - 1, t.length - 1);

  // i 长串、j 短串
  function helper(i, j) {
    if (j < 0) return 1;
    if (i < 0) return 0;

    if (memo[i][j] !== Infinity) return memo[i][j];

    memo[i][j] = s[i] === t[j]
      ? helper(i - 1, j) + helper(i - 1, j - 1)
      : helper(i - 1, j);
    return memo[i][j];
  }
};

从头往后：

var numDistinct = function (s, t) {
  const memo = Array.from(new Array(s.length), () => new Array(t.length).fill(Infinity));
  dfs(0, 0);
  console.log(memo);
  return memo[0][0];

  function dfs(longer, smaller) {
    if (smaller === t.length) return 1;
    if (longer === s.length) return 0;

    if (memo[longer][smaller] !== Infinity) return memo[longer][smaller];

    memo[longer][smaller] = t[smaller] === s[longer]
      ? dfs(longer + 1, smaller) + dfs(longer + 1, smaller + 1)
      : dfs(longer + 1, smaller);
    
    return memo[longer][smaller];
  }
};

方法三：动态规划

定义 dp

dp[i][j]：从开头到 s[i-1] 的子串中，出现『从开头到 t[j-1] 的子串』的次数。即：前 i 个字符的 s 子串中，出现前 j 个字符的 t 子串的次数。

状态转移方程：

当 s[i-1] != t[j-1] 时，有 dp[i][j] = dp[i-1][j];
当 s[i-1] == t[j-1] 时，有 dp[i][j] = dp[i-1][j-1] + dp[i-1][j]

初始化：

j==0 时，dp[i][0] = 1
i==0 时，dp[0][j] = 0

var numDistinct = function (s, t) {
  const dp = Array.from(new Array(s.length + 1), () => new Array(t.length + 1).fill(0));

  for (let i = 0; i <= s.length; i++) {
    dp[i][0] = 1;
  }

  for (let i = 1; i <= s.length; i++) {
    for (let j = 1; j <= t.length; j++) {
      dp[i][j] = s[i - 1] === t[j - 1]
        ? dp[i - 1][j - 1] + dp[i - 1][j]
        : dp[i - 1][j]
    }
  }
  return dp[s.length][t.length];
};

583. 两个字符串的删除操作

583. 两个字符串的删除操作
0615，mid，answer
动态规划

解析1：https://leetcode.cn/problems/edit-distance/solution/bian-ji-ju-chi-mian-shi-ti-xiang-jie-by-labuladong/
解析2：https://programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html
解析3：https://leetcode.cn/problems/delete-operation-for-two-strings/solution/gong-shui-san-xie-cong-liang-chong-xu-li-wqv7/

题目的要求是 word1 和 word2 各自选择一些字符，得到的字符串尽可能长。这就是求最长公共子序列，这里求的是最少的改变次数，也就是得出最长公共子序列，两个字符串一共要删掉多少个字符。

先求出最长公共子序列 max，然后再让 word1 和 wrod2 当长度分别剪去 max，就是最少删除次数。

定义 dp

dp[i][j]：长度为 [0, i - 1] 的字符串 word1 与长度为 [0, j - 1] 的字符串 word2 的最长公共子序列为 dp[i][j]。

定义状态转移方程

注意：因为是判断 [0, i - 1] 和 [0, j - 1] 这个区间，所以当前判断点位应当是 i - 1 和 j - 1。

case1：word1[i - 1] 与 word2[j - 1] 相同

找到了一个公共元素，所以两个字符串都前进一位， dp[i][j] = dp[i - 1][j - 1] + 1

case2：word1[i - 1] 与 word2[j - 1] 不相同

则让 word1 或 word2 其中一个前进一位，谁的最长公共子序列更长，就选谁：Math.max(dp[i - 1][j], dp[i][j - 1])

var minDistance = function (word1, word2) {
  const dp = Array.from(new Array(word1.length + 1), () => new Array(word2.length + 1).fill(0));

  for (let i = 1; i <= word1.length; i++) {
    for (let j = 1; j <= word2.length; j++) {
      dp[i][j] = word1[i - 1] === word2[j - 1]
        ? dp[i - 1][j - 1] + 1
        : Math.max(dp[i - 1][j], dp[i][j - 1]);
    }
  }
  // 求出最长子序列长度，然后让两者字符串分别剪掉长度，就得出最少变化：
  const max = dp[word1.length][word2.length];
  return word1.length - max + word2.length - max;
};

72. 编辑距离

72. 编辑距离
0615，hard，answer 没理解透
动态规划、递归

定义 dp

dp[i][j]，表示以下标 i-1 为结尾的字符串 word1，转化为以下标 j-1 为结尾的字符串 word2 的最少操作步骤

有四种操作步骤：跳过、插入、删去、替换。

状态转移方程：

（1）相等

如果 word1[i- 1] 和 word2[j - 1] 两个位置相等，则匹配成功，两个字符串都进行下一个匹配，总操作次数不变：
dp[i - 1][j - 1] ，下一次判断：word1[i] 和 word2[j]
回顾 dp 定义 dp[i-1][j-1]，表示以下标 i-2 为结尾的字符串 word1，转化为以下标 j-2 为结尾的字符串 word2 的最少操作步骤。在此基础上，因为 word[i-1] 和 wrod[i-2] 形成匹配。那么 dp[i - 1][j - 1] 就是 dp[i-1][j-1] +1。

（2）不相等

插入：word1 需要插入一个字符来和 word2[ j - 1] 进行匹配。

那么结果是：

word1[i-1] 不参与本次判断，参与下一次判断，判断位置不变，下一次判断 word[i-1]；
word2[j-1] 被新插入的字符匹配成功，不再参与下一次判断，下一次判断 word[j]；
操作总次数 + 1

构成逻辑：dp[i][j-1] + 1

回顾 dp 定义 dp[i][j-1]，表示以下标 i-1 为结尾的字符串 word1，转化为以下标 j-2 为结尾的字符串 word2 的最少操作步骤。
回顾 dp 定义 dp[i][j]，表示以下标 i-1 为结尾的字符串 word1，转化为以下标 j-1 为结尾的字符串 word2 的最少操作步骤。

通过上面的对比，我们知道 dp[i][j-1] 相比 dp[i][j]，字符串 word1 的判断区间没有变化，字符串 word2 的判断区间减少了一位。

删除：word1 既然 word1[i-1] 和 word2[j-1] 不匹配，那么就删除 word[i-1]，看看 word[i] 是否匹配：

word1[i-1] 被删除了，其实就是该点被判断过了，下一次遍历需要判断 word[i] 。而 word2[j-1] 没有被匹配掉，下次依然需要匹配这个位置，总操作次数 + 1。

替换：word[i-1] 直接换成 word[j-1] 这个值，然后让他们进行匹配。

那么这两个位置都被判断了，下一次遍历时判断 word1[i] 和 word[j]，总操作次数 + 1。

（3）初始化

如果 word2 已经遍历完，word1 还有剩余，那么 word1 剩余的操作就是全部删除（次数 = word1 剩余的个数）；
如果 word1 已经遍历完，word2 还有剩余，那么 word1 剩余的操作就是全部插入（次数 = word1 剩余的个数）；

dp[x][0] 表示当 word2 为 0 时，word1 的删除操作，word1 剩余 x 个就操作 x 次：dp[x][0] === x；

dp[0][x] 表示当 word1 为 0 时，word1 的插入操作，word2 剩余 x 个就操作 x 次：dp[0][x] === x；

var minDistance = function (word1, word2) {
  const dp = Array.from(new Array(word1.length + 1), () => new Array(word2.length + 1).fill(0));
  // 初始化
  for (let i = 0; i <= word1.length; i++) dp[i][0] = i;
  for (let j = 0; j <= word2.length; j++) dp[0][j] = j;

  for (let i = 1; i <= word1.length; i++) {
    for (let j = 1; j <= word2.length; j++) {
      // 相等，不操作，总数不变，各自增加一位
      if (word1[i - 1] === word2[j - 1])
        dp[i][j] = dp[i - 1][j - 1];
      else // 不相等：插入、删除、替换
        dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1], dp[i - 1][j - 1]) + 1;
    }
  }
  return dp[word1.length][word2.length];
};

3. 无重复字符的最长子串

3. 无重复字符的最长子串
0615，mid，answer
滑动窗口

用 map 记录不同值的位置，遇到位置冲突的，登记最靠右的位置。

[left, i] 区间构成的子串，就是一个无重复字符的最后子串。

当遇到重复字段时：
- 如果是 'aabcdab'。i 为 4 时，left 指向 1；当 i = 5 时，出现重复，map.get 返回 2，left 自然是 map.get(s[5]) + 1；
- 如果时 'abcbda'。i 为 4 时，left 指向 2 (子串：cbd)；当 i = 5 时，出现重复， map.get(s[5]) + 1 值为 1，比 left 小；说明 left 已经因为曾经出现重复（字母b）更新过一次，这里继续用 left，而不是 map.get(s[5]) + 1 。

var lengthOfLongestSubstring = function (s) {
  if (s.length === 0) return 0;
  // 滑动窗口 [left, i] 闭口
  let left = 0;
  let res = 0;
  const map = new Map();

  for (let i = 0; i < s.length; i++) {
    // 重复,调整left：Math.max(当前位置，重复位置右边1位)
    if (map.has(s[i]))
      left = Math.max(left, map.get(s[i])+ 1) ;

    map.set(s[i], i);
    res = Math.max(res, i - left + 1);
  }
  return res;
};

647. 回文子串

方法一：动态规划

讲的非常清楚：🔍。

定义 dp

布尔类型的 dp[i][j]：表示区间范围 [i,j] （左闭右闭）的子串是否是回文子串，如果是 dp[i][j] 为true。

确定状态转移方程

在确定递推公式时，就要分析如下几种情况。

整体上是两种，就是 s[i] 与 s[j] 相等，s[i] 与 s[j] 不相等这两种。

当 s[i] 与 s[j] 不相等，dp[i][j] 为 false，这不是个回文串。

当 s[i] 与 s[j] 相等时，有如下三种情况：

情况一：下标 i 与 j 相同，同一个字符例如 a，是回文子串
情况二：下标 i 与 j 相差为1，例如 aa，是回文子串
情况三：下标：i 与 j 相差大于 1，例如 cabac，此时 s[i] 与 s[j] 已经相同了，i 到 j 区间是不是回文子串就看 aba 是不是回文就可以了，那么 aba 的区间就是 [i+1, j-1]，这个区间是不是回文就看 dp[i + 1][j - 1] 是否为 true。

初始化

dp[i][j] 初始化为 false。

确定遍历顺序

从递推公式中可以看出，情况三是根据 dp[i + 1][j - 1] 是否为 true，在对 dp[i][j] 进行赋值 true 的。

dp[i + 1][j - 1] 在 dp[i][j] 的左下角，如图：

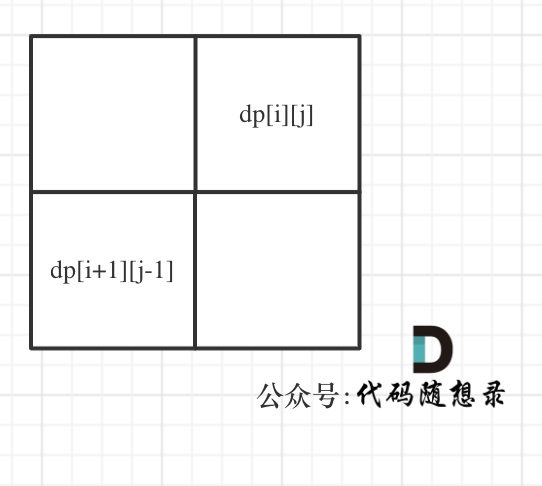
647.回文子串

所以一定要从下到上，从左到右遍历，这样保证 dp[i + 1][j - 1] 都是经过计算的。

注意，j 从 i 开始遍历，因为 j 作为 [i, j] 的右区间，一定比 i 大。

var countSubstrings = function (s) {
  const dp = Array.from(new Array(s.length), () => new Array(s.length).fill(false));
  let res = 0;

  // dp[i][j]依赖于dp[i+1][j-1]，从下往上、从左往右遍历
  for (let i = s.length - 1; i >= 0; i--) {
    for (let j = i; j < s.length; j++) { // 区间[i,j]告诉我们，j只会比i大
      // 不相等默认为 false      
      // 相等，[i,j]子串的长度 <= 3
      // 相等，左右各减少一个的[i+1, j-1]子串也为true
      if (s[i] === s[j] && (j - i <= 2 || dp[i + 1][j - 1])) {
        res++;
        dp[i][j] = true;
      }
    }
  }
  return res;
};

方法二：双指针

从头到尾完整遍历一遍 string，以每一个成员 i 为核心，左右扩展判断有几个回文子串：

分两种情况：

以 i 为核心左右扩展
以 i , i+1 两个数字为核心左右扩展

var countSubstrings = function (s) {
  let res = 0;
  for (let i = 0; i < s.length; i++) {
    res += palindromic(i, i);
    if (s[i] === s[i + 1]) res += palindromic(i, i + 1);
  }
  return res;

  function palindromic(i, j) {
    let sum = 0;
    while (i >= 0 && j <= s.length && s[i] === s[j]) {
      i--, j++, sum++;
    }
    return sum;
  }
};

516.最长回文子序列

516. 最长回文子序列
0615，mid，answer
动态规划

定义dp

dp[i][j]：字符串 s 在 [i, j] 范围内最长的回文子序列的长度为 dp[i][j]。

定义状态转移方程

如果 s[i] 与 s[j] 相同，那么 dp[i][j] = dp[i + 1][j - 1] + 2;
如果不相同，那么跳过 i，或者跳过 j 继续判断。
- dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);

初始化

长度为 1 一定是回文串，其余都不是，所以把 dp[x][x] 赋值为 1；

遍历范围

和上一题一样，dp[i][j] 依赖于 dp[i+1][j-1]，遍历从下至上，从左至右。

额外注意：j 从 i + 1 开始，因为 i == j 已经初始化的时候赋值了，是 base case。dp[i+1][j-1] 的判断源头依赖于 dp[i][i]。

var longestPalindromeSubseq = function (s) {
  // dp[i][j]：区间[i, j] 的一个最长回文序列的大小
  const dp = Array.from(new Array(s.length), () => new Array(s.length).fill(0));
    // 初始化
  for (let i = 0; i < s.length; i++) dp[i][i] = 1;

  // dp[i][j]依赖于dp[i+1][j-1]，遍历从下至上，从左至右
  for (let i = s.length - 1; i >= 0; i--) {
    for (let j = i + 1; j < s.length; j++) {
      dp[i][j] = s[i] === s[j]
        ? dp[i + 1][j - 1] + 2  // 相等，则长度 + 2
        : Math.max(dp[i + 1][j], dp[i][j - 1]); // 不相等，则i跳过，或者j跳过
    }
  }
  return dp[0][s.length - 1];
};

198. 打家劫舍​

方法一：二维dp​

方法二：一维dp​

方法三：一维dp｜滚动数组​

213. 打家劫舍 II​

方法一：一维dp​

方法二：一维dp｜滚动数组​

337. 打家劫舍 III​

方法一：记忆化递归​

方法二：动态规划​

121. 买卖股票的最佳时机​

方法一：贪心​

方法二：动态规划｜滚动数组​

122. 买卖股票的最佳时机 II​

方法一：动态规划｜滚动数组​

123. 买卖股票的最佳时机 III​

方法二：一维dp｜滚动数组​

188. 买卖股票的最佳时机 IV​

方法一：二维dp数组​

方法二：一维dp数组​

309. 最佳买卖股票时机含冷冻期​

714. 买卖股票的最佳时机含手续费​

300. 最长递增子序列​

674. 最长连续递增序列​

方法一：一维dp​

方法二：滚动数组​

718. 最长重复子数组​

方法一：二维dp​

方法二：一维dp​

1143.最长公共子序列​

1035. 不相交的线​

53. 最大子数组和​

方法一：贪心​

方法二：动态规划​

392. 判断子序列​

方法一：动态规划​

方法二：双指针​

115. 不同的子序列​

方法一：dfs 递归​

方法二：递归｜记忆化搜索​

方法三：动态规划​

583. 两个字符串的删除操作​

72. 编辑距离​

3. 无重复字符的最长子串​

647. 回文子串​

方法一：动态规划​

方法二：双指针​

516.最长回文子序列​

198. 打家劫舍

方法一：二维dp

方法二：一维dp

方法三：一维dp｜滚动数组

213. 打家劫舍 II

方法一：一维dp

方法二：一维dp｜滚动数组

337. 打家劫舍 III

方法一：记忆化递归

方法二：动态规划

121. 买卖股票的最佳时机

方法一：贪心

方法二：动态规划｜滚动数组

122. 买卖股票的最佳时机 II

方法一：动态规划｜滚动数组

123. 买卖股票的最佳时机 III

方法二：一维dp｜滚动数组

188. 买卖股票的最佳时机 IV

方法一：二维dp数组

方法二：一维dp数组

309. 最佳买卖股票时机含冷冻期

714. 买卖股票的最佳时机含手续费

300. 最长递增子序列

674. 最长连续递增序列

方法一：一维dp

方法二：滚动数组

718. 最长重复子数组

方法一：二维dp

方法二：一维dp

1143.最长公共子序列

1035. 不相交的线

53. 最大子数组和

方法一：贪心

方法二：动态规划

392. 判断子序列

方法一：动态规划

方法二：双指针

115. 不同的子序列

方法一：dfs 递归

方法二：递归｜记忆化搜索

方法三：动态规划

583. 两个字符串的删除操作

72. 编辑距离

3. 无重复字符的最长子串

647. 回文子串

方法一：动态规划

方法二：双指针

516.最长回文子序列