6. 二叉树2
700. 二叉搜索树中的搜索
- 700. 二叉搜索树中的搜索
- 0429,easy,answer
- 注意递归返回的时机(return)
方法一:递归
- 注意对值的判断是在函数的返回体中。
var searchBST = function (root, val) {
// 找不到,返回null
// 找到了,返回 root
if (!root || val === root.val) return root;
// 如果 val < 根值,则递归左子树;否则递归右子树
return val < root.val
? searchBST(root.left, val)
: searchBST(root.right, val);
};
方法二:迭代
var searchBST = function (root, val) {
while (root) {
if (!root || val === root.val) break;
root = val < root.val
? searchBST(root.left, val)
: searchBST(root.right, val);
}
return root;
}
98. 验证二叉搜索树
- 98. 验证二叉搜索树
- 0429,mid,answer
- 中序遍历、二叉搜索树的复习
中序遍历下,输出的二叉搜索树节点的数值是有序序列。
- 判断中序遍历的结果是否是一个递增数列。
方法一:中序遍历 |递归
- 注意递归函数是否需要返回值,根源是这个递归函数的作用是什么:
- 本题中 dfs 的作用是判断入参 node 节点是否是一个二叉搜索树,应当返回 true 和 false;
- 当达到叶子结点的时候,这里卡了很久。其实明白叶子结点也是一个二叉搜索树,应当返回 true。
var isValidBST = function (root) {
if (!root) return true;
// 中序遍历出的二叉搜索树,是一个递增的有序数列,
// 不需要保存一个数列,我们只需要判断递归出来第 k 个数 > k-1 个数,就是递增的,否则返回 false;
let preVal;
return dfs(root);
function dfs(node) {
// 左
const leftRes = node.left ? dfs(node.left) : true;
// 根
// 判断第一个数时,没有 preVal,所以要判断不是 undefined
// 非增序:返回 false 结束递归
if (preVal !== undefined && node.val <= preVal) return false;
// 增序:符合预期,替换 preVal
preVal = node.val;
// 右
const rightRes = node.right ? dfs(node.right) : true;
return leftRes && rightRes;
}
};
方法二:中序遍历 | 迭代 |通用方法
var isValidBST = function (root) {
if (!root) return true;
let pre = -Infinity;
const stack = [root];
while (stack.length) {
const node = stack.pop();
// 通用法左、中、右,遇到中先放null,下次遇到读取值。
if (node === null) {
val = stack.pop().val;
if ( pre < val) {
pre = val;
continue;
}
return false;
}
// 右
if (node.right) stack.push(node.right);
// 中
stack.push(node);
stack.push(null);
// 左
if (node.left) stack.push(node.left);
}
return true;
};
方法三:中序遍历|迭代
var isValidBST = function (root) {
// 迭代: 中序遍历的传统方法
// 先遍历到最左叶子结点,然后回溯到根结点,然后遍历右节点
// 指针访问
if (!root) return false;
const stack = [];
let cur = root;
let pre = -Infinity;
while (stack.length || cur) {
// 深度遍历左
while (cur !== null) {
stack.push(cur);
cur = cur.left;
}
cur = stack.pop();
// 回溯中
if (pre >= cur.val) {
return false;
}
pre = cur.val
// 遍历一次右
cur = cur.right;
}
return true;
};
530. 二叉搜索树的最小绝对差
- 530. 二叉搜索树的最小绝对差
- 0430,easy,quick
- 中序遍历的复习
二叉搜索树问题转化为有序数组问题
- pre 和 cur 求最小差绝对值
中序遍历的三种方法:
- 递归、迭代、通用迭代
方法一:中序遍历|迭代
- 迭代: 用指针控制下一个遍历元素
var getMinimumDifference = function (root) {
const stack = [];
let cur = root;
let pre;
let res = Infinity;
while (stack.length || cur !== null) {
// 指针指向了node,则遍历这个node的左节点。
// 指针指向了null,则没有左节点了,开始回溯遍历根和右节点。
while (cur !== null) {
stack.push(cur);
// 左
cur = cur.left;
}
cur = stack.pop();
// 中
if (pre !== undefined) {
res = Math.min(res, cur.val - pre);
};
pre = cur.val;
// 右
cur = cur.right
}
return res;
};
方法二:中序遍历|通用迭代
- while 循环有两种执行:
- 读取根结点值:判断 node === null,则stack 中下一个节点出栈,并读取值。
- 迭代:分别右、中(+null)、左挨个入栈。
- 注意:stack 结构,左右对换,从 右 开始。
var getMinimumDifference = function (root) {
const stack = [root];
let pre;
let res = Infinity;
while (stack.length) {
let node = stack.pop();
// 如果有null,则证明应该读取根了,然后这轮while循环就是读取根,读取根后continue。
if (node === null) {
cur = stack.pop().val;
if (pre !== undefined) {
res = Math.min(res, cur - pre);
}
pre = cur;
continue;
}
// 右
node.right && stack.push(node.right);
// 中,遇到放入node,放入null
stack.push(node);
stack.push(null);
// 左
node.left && stack.push(node.left);
}
return res;
};
方法三:中序遍历|递归
var getMinimumDifference = function (root) {
let pre;
let res = Infinity;
dfs(root);
// 遍历所有的node
function dfs(node) {
// 左、中、右
node.left && dfs(node.left);
if (pre !== undefined) {
res = Math.min(res, node.val - pre);
}
pre = node.val;
node.right && dfs(node.right);
}
return res;
};
501. 二叉搜索树中的众数
- 501. 二叉搜索树中的众数
- 0430,easy,answer
- 二叉搜索树、中序遍历、众数
主要的难点是对题目的认知,题目要求出现频率最高的众数,如果有多个频率相同的众数,就返回多个。
- 结果是 n 个,不是只有一个;
- 不要通过一个长数组维护全部众数的频率,而是:
- 用 pre 去判断当前遍历的数值是否发生改变,从而可以得出 pre 值的出现频率 count;
- 用 count 统计 pre 值的出现频率;
- 用 maxCount 维护当前结果的频率(遍历时,到当前为止的最大频率,但不一定是结果的最大频率);
- 如果 count > maxCount 则需要重置 maxCount,清空 res。
- 用 res 维护一个数组,成员是多个最大频率相同的值。
方法一:中序遍历|递归
- 也可以使用 迭代、通用迭代两种方法,只是中序遍历方式的改变,对众数的判断一模一样,不在此列出了。
var findMode = function (root) {
if (root === null) return 0;
// res中的最大频率、当前的频率
let maxCount = 0;
let count = 0;
// 上一个结点值、最高频率元素集合
let pre = root.val;
let res = [];
dfs(root);
return res;
// 递归
function dfs(node) {
// 左
node.left && dfs(node.left);
// 中:判断众数
// 计算count,相等则加1,不等则重置为1
if (node.val === pre) count++;
else count = 1;
pre = node.val;
// 比较count,
// 大于maxcount:重置 maxCount、res,并将当前值放入新res,
// 等于maxcount:当前值放入res
// 小于maxcount:丢弃不操作
if (count > maxCount) {
maxCount = count;
res = [node.val];
} else if (count === maxCount) {
res.push(node.val);
}
// 右
node.right && dfs(node.right);
}
}
236. 二叉树的最近公共祖先
- 236. 二叉树的最近公共祖先
- 0430,mid,answer
- 最近公共祖先的概念、后序遍历、自底向上
要点:
理解最近公共祖先的概念:
- 两个结点共同的根、这根深度尽可能深。
- 公共祖先有可能是A、B节点本身。
公共祖先因为要找最深的节点,适用于后序遍历(天然的自底向上查找)。
后序遍历的特点:对于一个最小单位树(3个结点),依次遍历左、右,最后才是中。所以根结点的左树和右树是先遍历的。
回溯,当遍历到要找的 A、B结点时,会通过 回溯把这个消息告诉父节点。
- 所以:用递归时,出现第一个结点的 left 或 right 树遍历到了 A、B 结点,那这个节点就应当是要找的最近公共祖先。
var lowestCommonAncestor = function (root, p, q) {
// 后序遍历
return dfs(root);
// 需要返回值:如果找到 p、q 则返回节点本身,否则返回 false
// 会遍历整个数,把结果及时回溯。
function dfs(root) {
// 遇到节点为空、p、q,就返回节点本身
if (!root || root === p || root === q) return root;
//左
const left = dfs(root.left);
//右
const right = dfs(root.right);
//中
// 如果left、right都有值,说明当前root节点就是最近公共祖先,返回root
if (left && right) return root;
// 如果只有一边有值,则向上回溯,只返回有值的一边
return left ? left : right ? right : false;
}
};
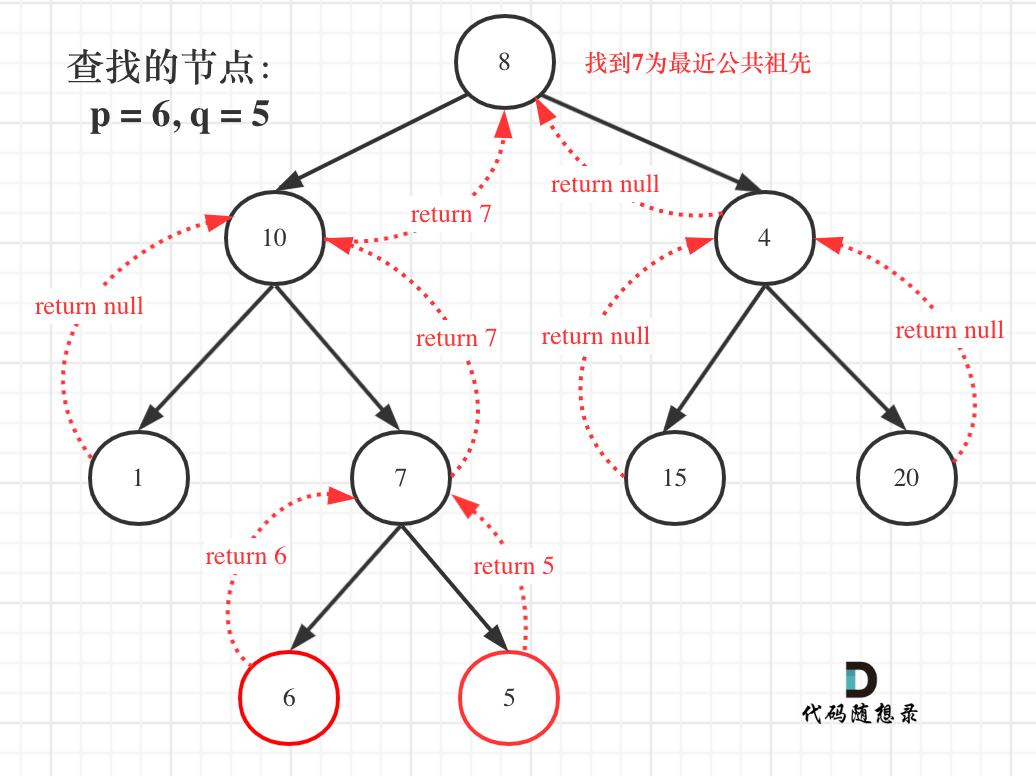
思考,如果查找的是 6 和 7,其最近公共祖先就是 7 本身。
自然的,当我们遍历到 7 这个根结点时,会先执行:
// 遇到节点为空、p、q,就返回节点本身
if (!root || root === p || root === q) return root;所以 7 会直接向上返回 7 本身,然后一路回溯到根结点,得到答案 7。是符合预期的。
235. 二叉搜索树的最近公共祖先
- 235. 二叉搜索树的最近公共祖先
- 0430,easy,answer
- 二叉搜索树的特点
本题:遍历已经不是一个二叉树了,其实更像是一个数组,当满足条件时及时返回遍历的结果。
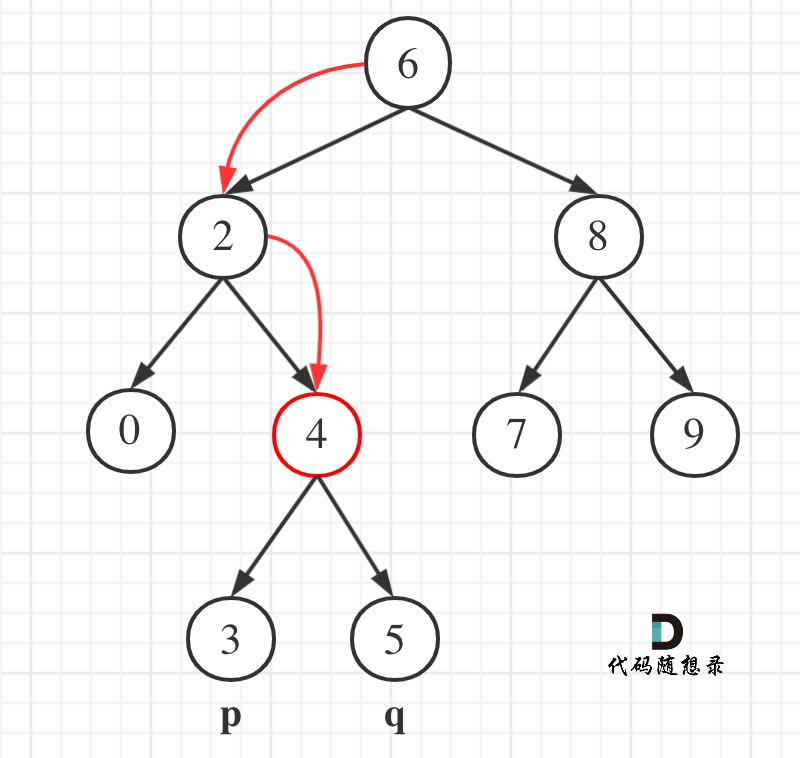
二叉搜索树自带方向性:
- 可以看上图,如果查找 3 和 5,相比上一题 501,只要我们判断某一个节点位于
[3, 5]之间就可以了。
具体来讲:
- 不再需要回溯,遍历到一个节点时,直接判断:
- 如果当前节点值比 q 和 p 都小,那么下一步需要遍历 left 子树,放弃 right 子树。
- 反之,如果当前节点值更大,那么下一步便利 right 子树。
- 最后,如果当前节点处在
[p, q]区间之间(可以等于 p 或 q),左闭右闭区间,那么得到答案,返回这个节点。
方法一:递归
- return 写在 左、右子树的遍历上,则每次调用
dfs只会遍历其中的一边。且如果一旦命中了return root递归就会结束,携带着 root 节点一路向上 return,最终返回的结果就是 root。
// 返回:q、p的公共祖先 root
var lowestCommonAncestor = function (root, p, q) {
if (!root) return root;
const val = root.val;
// 左,查找左子树
if (val > p.val && val > q.val) {
// 如果没有左子树,则证明找不到返回null
return lowestCommonAncestor(root.left, p, q);
}
// 右,查找右子树
if (val < p.val && val < q.val) {
// 如果没有右子树,则证明找不到返回null
return lowestCommonAncestor(root.right, p, q);
}
return root;
};
方法二:迭代
- 不是传统的遍历迭代方式,还是记住上面的图。遍历已经不是一个二叉树了,其实更像是一个数组,当满足条件时及时返回遍历的结果。
var lowestCommonAncestor = function (root, p, q) {
while (root) {
const val = root.val;
// 左,查找左子树
if (val > p.val && val > q.val) {
root = root.left;
// 右,查找右子树
} else if (val < p.val && val < q.val) {
root = root.right;
} else {
// 找到值
return root;
}
}
return null;
};
701. 二叉搜索树中的插入操作
- 701. 二叉搜索树中的插入操作
- 0501,mid,quick
对于如下二叉树,如果要插入 5,从 root 开始比较节点大小。
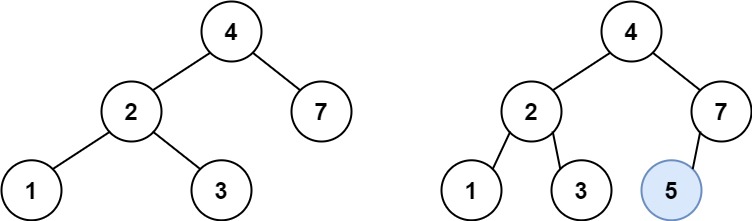
遍历节点,如果便利到 node 值 > 要插入的 val。则继续遍历 node.left,反之遍历 node.right。
- 这相当于每次面对一个小二叉树时,只选择其中一个分支遍历。
方法一:迭代,我的方法
- 利用 cur 指向当前遍历的节点,pre 指向他上一个遍历的节点。
- 当 cur 遍历到 null 时,表明这是一个插入位置,然后用 pre 进行插入。
问:pre 的作用是什么?
- cur 如果指向了 null,此时 cur 已经不再指向 root 树中的任何一个节点了,无法对 root 进行增加节点的操作。所以要用 pre 指向 cur 遍历的上一个节点,然后当 cur 指向 null,表明此时可以在 pre 上增加节点了。
- 虽然知道要在 pre 上增加节点了,但不清楚是 .left 还是 .right 上添加,这时候需要再进行一次判断。
var insertIntoBST = function (root, val) {
if (!root) return new TreeNode(val);
let cur = root;
let pre = null;
while (cur !== null) {
pre = cur;
cur = cur.val > val ? cur.left : cur.right;
}
// 对 pre 进行判断,确定是在左子树还是右子树上添加新节点
pre.val > val ? pre.left = new TreeNode(val) : pre.right = new TreeNode(val);
return root;
};
方法二:递归
可以看到,如果使用迭代,需要用 pre 指针保留 cur 遍历到的上一个节点,方便后续的插入操作。
- cur 一旦遍历到 null,则不再指向 root 中任何一个节点了,换句话说 cur 无法再控制 root 了,必须要用另一个指针 pre “留在” root 上。
- 自上而下的递归。使用递归返回值 return ,让父节点等待一个字节点返回回来并绑定到对应的子树上,可以解决多一个 pre 的问题:
总结:
返回值:利用返回值完成新加入的节点与其父节点的赋值操作。换句话说,父节点在 root.left 或 root.right 等待一个子节点,这个子节点可能是新插入的节点,也可能是和之前一样的节点。
终止条件:遍历的节点为 null 时,找到要插入节点的位置,把插入的节点返回。
var insertIntoBST = function (root, val) {
// 找到合适的放置位置
if (root === null) {
return new TreeNode(val);
}
// 判断是左子树还是右子树
root.val > val
? root.left = insertIntoBST(root.left, val)
: root.right = insertIntoBST(root.right, val);
return root;
};
450. 删除二叉搜索树中的节点
- 450. 删除二叉搜索树中的节点
- 0501,mid,answer
- 了解二叉树的删除方法、了解二叉搜索树的删除特点、
- 利用 pre 和 cur 锁定节点、利用 while 找到叶子结点
方法一:迭代
两个步骤:
- 找到要删除的元素 cur,和他的父节点 pre;
- pre 如果为 null,择表明要删除的是根结点本身;
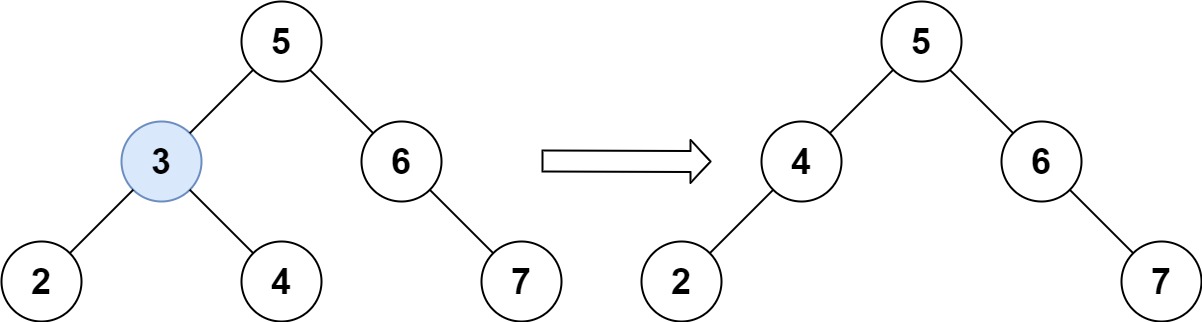
- 删除 cur,并把 cur 的子树按照搜索二叉树的规则放好:
cur.left一定是比cur.right的所有值都要小;cur.right中的最小值一定是该子树的最左下角叶子结点;- 所以
cur.left要放置在cur.right的最左下角叶子结点下即可。
var deleteNode = function (root, n) {
if (!root) return null;
let cur = root;
let pre = null;
// 找带删除节点
while (cur !== null) {
if (cur.val === n) break;
pre = cur;
cur.val > n ? cur = cur.left : cur = cur.right;
}
// 此时:cur指向待删除节点,pre指向cur的父节点
// 通过pre确定删除父元素
// pre为null,说明cur是根结点
if (pre === null) return delNode(cur);
pre.val > n ? pre.left = delNode(cur) : pre.right = delNode(cur);
return root;
// 删除node节点
// 总体来说,就是要把node.left按照搜索二叉树的规定,放到node.right上,然后返回node.right;
// 删除node时,要把node.left放到node.right.left.left.left...下(根据搜索二叉树的定义)
function delNode(node) {
if (!node) return node;
if (!node.right) return node.left;
let cur = node.right;
// 找到 node.right.left.left...
while (cur.left) {
cur = cur.left;
}
cur.left = node.left
// 返回 node.right
return node.right;
}
}
方法二:递归
- 将迭代改造为递归,其实更简单了:
var deleteNode = function (root, n) {
if (!root) return root
// 定位到目标结点
if (root.val === n) return delNode(root);
// 没定位到继续递归
root.val > n
? root.left = deleteNode(root.left, n)
: root.right = deleteNode(root.right, n)
return root
// 和迭代中的方法相同
function delNode(node) {
if (!node) return node;
if (!node.right) return node.left;
let cur = node.right;
// 找到 node.right.left.left...
while (cur.left) {
cur = cur.left;
}
cur.left = node.left
// 返回 node.right
return node.right;
}
}
669. 修剪二叉搜索树
- 669. 修剪二叉搜索树
- 0501,mid,answer
- 二叉树的特性,递归返回的时机、递归返回值的确定
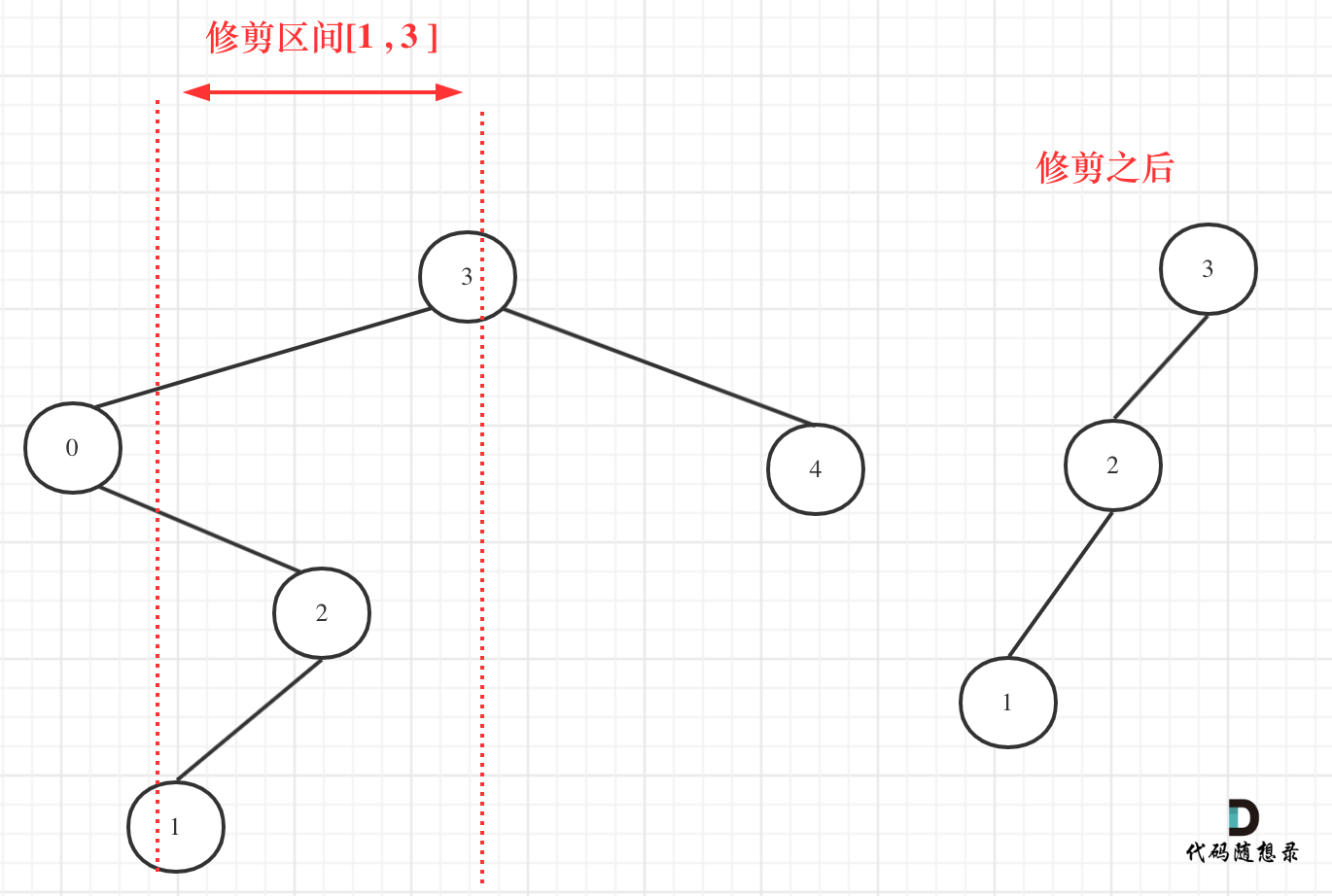
上图可以直观的看到,当一个区间是 [1, 3] 时,把 1 和 4 节点抛弃了。代码随想录
搜索二叉树的修剪,一定是图中那样,把不符合区间的左右分支抛弃掉。
- 搜索二叉树的特点:
- 一个节点的左子树的所有成员,一定大于节点本身;
- 一个节点的右子树的所有成员,一定大于节点本身;
- 所以,当由顶向下遍历到某个 node 时,如果
node.val < low,那么这个节点需要被抛弃了,随之它的node.left也要被抛弃,但它的node.right中可能有大于 low 的子树不能被抛弃。
递归 trimBST:
- 返回值:返回一个经过修剪的,符合条件的子树。所以每一个 node 节点的遍历,都会在
node.left和node.right等待一个返回值,最终也会返回修剪好的 node 节点自身。 - 当节点自身不符合
[low, high]区间内时,则自身不能被返回。- 此时返回
node.left或者node.right中符合条件的子树。
- 此时返回
方法一:递归
var trimBST = function (root, low, high) {
if (!root) return root;
// 如果比low小,从 root.right 找到符合条件的子树返回,其余的节点全部抛弃
if (root.val < low) {
return trimBST(root.right, low, high);
}
// 如果比high大,从 root.left 找到符合条件的子树返回,其余的节点全部抛弃
if (root.val > high) {
return trimBST(root.left, low, high);
}
// 执行到这里,说明 node.val 在[low,high]区间内,递归左右子树,返回自身节点
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
return root
};
方法二:迭代|暂时不看
搜索二叉树的修剪,一定是图中那样,把不符合区间的左右分支抛弃掉。
- 这是上图得出的结论,所以迭代的主要思想是:
- 先确定符合
[low,high]区间的根结点 resNode; - 然后 while 循环
res.left找到符合条件的左子树; - 最后 while 循环
res.right找到符合条件的右子树;
- 先确定符合
var trimBST = function (root, low, high) {
if (!root) return root;
let cur = root;
// 找到符合条件的根结点,处在 [low, high] 区间内
while (cur !== null && (cur.val < low || cur.val > high)) {
if (cur.val < low) cur = cur.right;
if (cur.val > high) cur = cur.left;
}
// 此时cur指向符合条件[low,high]的root节点,resNode就是最后要返回的节点
const resNode = cur;
// 处理左子树
while (cur !== null) {
// 让 cur.left 处在[low,high] 区间
while (cur.left && cur.left.val < low) cur.left = cur.left.right;
// cur.left 处在 [low, high] 区间循环处理 cur.left.left
cur = cur.left;
}
// 与resNode.left同理,处理resNode.right
cur = resNode;
while (cur !== null) {
while (cur.right && cur.right.val > high) cur.right = cur.right.left;
cur = cur.right;
}
// 如果比low小,从 root.right 找到符合条件的子树返回,其余的节点全部抛弃
if (root.val < low) {
return trimBST(root.right, low, high);
}
return resNode;
};
108. 将有序数组转换为二叉搜索树
- 108. 将有序数组转换为二叉搜索树
- 0501,easy,quick
- 平衡二叉树、二叉搜索树、下标分割序列构造二叉树
方法一:递归
不断中间分割,然后递归处理左区间,右区间,也可以说是分治。
先从 “中序遍历一个二叉搜索树,得出的结果是一个递增序列” 这个规律入手。
- 中序遍历的特性是:左、中、右,要先确定序列中 根 的位置
index = Math.floor(nums.length / 2); - 然后通过 index 把序列切分为 左、右 两个部分,递归寻找
root.left和root.right子树。
确定递归:
- 递归返回值:根据序列构造好的子节点本身。
- 递归的结束:
- 序列 nums.length === 0,则返回 null,递归结束;
- 序列 nums.length === 1,index 计算结果为 0,刚好创建一个叶子结点返回。
var sortedArrayToBST = function (nums) {
if (nums.length === 0) return null;
// 求序列的中间树,为根 root.val
const index = Math.floor(nums.length / 2);
const root = new TreeNode(nums[index]);
// 递归获得左、右子树
root.left = sortedArrayToBST(nums.slice(0, index));
root.right = sortedArrayToBST(nums.slice(index + 1, nums.length));
// 返回构造好的子树
return root;
};
方法二:递归|优化空间
- 不需要每次对 nums 进行切割,递归函数 build 传入数组的下标 left 和 right 即可。
注意:
- 求
index时,不要忘记加上基数left; [left, right]是左闭右闭区间。
var sortedArrayToBST = function (nums) {
return build(nums, 0, nums.length - 1);
function build(nums, left, right) {
// 递归结束
if (left > right) return null;
// 根结点
const index = left + Math.floor((right - left) / 2);
const root = new TreeNode(nums[index]);
// 左右子树
root.left = build(nums, left, index - 1);
root.right = build(nums, index + 1, right);
// 返回
return root;
}
};
- 时间复杂度:O(n),其中 n 是数组的长度。每个数字只访问一次。
- 空间复杂度:O(logn),其中 n 是数组的长度。空间复杂度不考虑返回值,因此空间复杂度主要取决于递归栈的深度,递归栈的深度是 O(logn)。
- 为什么是 log?联想二分法:
- 第一次递归:数组长度为 n,有两个
left和right递归,则再乘以一个基数 2,但复杂度不考虑基数,所以直接忽略掉。 - 第二次递归:数组长度为 n / 2;
- 第三次递归:数组长度为 n / 2 * 2 == n / 4;
- ...
- 所以每次递归数组长度会减少一半。这样列出等式计算:有机会自己写一个
迭代太复杂,暂时不考虑。
538. 把二叉搜索树转换为累加树
0501,mid,quick
累加树特性、二叉搜索树特性、中序遍历
累加树中,每个节点 node 的值是原树中 大于等于 node.val 的值之和;
二叉搜索树中,中序遍历的序列是一个递增序列;
所以:如果一个二叉搜索树遍历出来的序列是:[3 ,8 ,11, 14] ,则累加树就是 [14, 25, 33, 36]。也就从最后一个节点(最大)往前累加即可。
方法一:递归|反中序遍历
反中序遍历,也就是遍历出的结果是递减的,有些遍历右下角的节点。
- 中序遍历:左、根、右;反中序遍历:右、根、左。
- 上面例子中,反中序遍历的结果就是:
[14, 11, 8, 3],累加后:[36, 33, 25, 14]。
递归需要整个树,不需要返回值。
需要 pre 节点指向当前节点的前一个节点,方便累加。
var convertBST = function(root) {
if (!root) return root;
let pre = null;
dfs(root);
return root;
function dfs(node) {
// 反中序遍历:右、中、左
node.right && dfs(node.right);
// 如果pre为null,则表明此时递归root结点,跳过累加
if (pre) node.val += pre.val;
pre = node;
node.left && dfs(node.left);
}
};
方法二:迭代|反中序遍历
有两种写法:指针写法和通用写法:
- 指针写法:
- 先 while 到左下角叶子结点,
- 然后回溯到父节点 node、遍历 node.right,
- 继续 while 到叶子结点
var convertBST = function (root) {
if (!root) return root;
let pre = null;
let cur = root
const stack = []; // stack 不预先放入root,stack未来只会放入.right的结点
while (cur !== null || stack.length) {
// 右
while (cur !== null) {
stack.push(cur); // 这里push(cur),不是push(cur.left)
cur = cur.right;
}
// 中
cur = stack.pop();
const ans = cur.val;
if (pre) cur.val += pre.val;
pre = cur;
console.log(ans, cur.val);
// 左
cur = cur.left;
}
return root;
};
方法三:统一迭代|反中序遍历
- 这个方法是真的慢,尽量还是记 “指针迭代” 的方法。
var convertBST = function (root) {
if (!root) return root;
let pre = null;
const stack = [root];
while (stack.length) {
const node = stack.pop()
// null, 读取值
if (!node) {
cur = stack.pop();
if (pre) cur.val += pre.val;
pre = cur;
continue;
}
// 反中序遍历的stack,左开始
// 左
node.left && stack.push(node.left);
// 中
stack.push(node);
stack.push(null);
// 右
node.right && stack.push(node.right);
}
return root;
};
- 二叉树结束:代码随想录。
=== Todo List ============================
0428 - 刚做完的几道题:124,543,988,70,437 找机会复习一下,最晚 5 天内:5月3日前。
0430 - 复习:236、501、530、700、236,5天内,5月5日前。
经验总结:
- 所有树的题目,都想成一颗只有根、左节点、右节点 的小树。然后一颗颗小树构成整棵大树,所以只需要考虑这颗小树即可。
- 可以不需要直接用 debugger,用 console.log() 在关键位置输出,也能及时的发现问题;
- 递归逻辑要按照以下逻辑来考虑:
- 入参、出参;
- 返回条件;
- 递归条件;
- 二叉搜索树的特点:
- 中序遍历,是一个递增序列。
- 反中序遍历(右、中左),是一个递减序列(538题)。
- 任意一个结点的左子树的结点,一定小于右子树的结点;
- 任意一个结点的左子树中,最大值是
node.left.right.right.right ...; - 任意一个结点的右子树中,最大值是
node.right.left.left.left...;
- 任意一个结点的左子树中,最大值是
=== 待确认 ===============================
- root 是一个节点,就算 val 是负,其本身应当也没有正负之分, root 还是会返回 true??
- 想判断
root是否为空,不能用!root,必须用root !== null因为有可能root的值是负的。
- 想判断