9. 动态规划(1)
动态规划(1)主要讲了动态规划基本题型 + 0 1 背包问题、完全背包问题
动态规划
定义三大步骤:
- 确定 dp 数组及下标的含义;
- 确定递推公式(状态转移方程);
- 执行:
- 初始化 dp 数组;
- 确定遍历顺序;
- 举例推导 dp 数组;
509. 斐波那契数
- 509. 斐波那契数
- 0608,easy,quick
- 动态规划
定义一个 dp 数组:
var fib = function (n) {
dp = [];
dp[0] = 0;
dp[1] = 1;
for (let i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
};
优化:将 dp 数组压缩为两个变量:
var fib = function (n) {
if (n === 0) return 0;
if (n === 1) return 1;
let f1 = 0, f2 = 1;
for (let i = 2; i <= n; i++)
[f2, f1] = [f2 + f1, f2];
return f2;
};
70. 爬楼梯
0608,easy,answer
动态规划
只有两种方法:跳一步和跳两步。所以,当要计算第 i 层有多少种方法时,如果已经知道第 i - 1 层有多少种方法;第 i - 2 层有多少种方法,相加即可。
- i - 2 层需要直接迈两步到当前楼层。不能迈一步,迈一步就成为
i - 1 层有多少种方法了
定义一个 dp 数组:
// dp[i] 爬到第i层楼梯,有多少方法:
const dp = [];
dp[1] = 1, dp[2] = 2;
for (let i = 3; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
};
优化:改为滚动数组
var climbStairs = function (n) {
// dp[i] 爬到第i层楼梯,有多少方法:
if (n <= 1) return n;
const dp = [];
dp[1] = 1;
dp[2] = 2;
for (let i = 3; i <= n; i++) {
const sum = dp[2] + dp[1];
dp[1] = dp[2], dp[2] = sum;
}
return dp[2];
};
746. 使用最小花费爬楼梯
0608,easy,quick
动态规划
复杂度:时间 / 空间 O(n)。
var minCostClimbingStairs = function (cost) {
// dp[i]:到达第i个台阶所花费的最少费用
const dp = [];
dp[0] = cost[0];
dp[1] = cost[1];
for (let i = 2; i < cost.length; i++) {
dp[i] = Math.min(dp[i - 2], dp[i - 1]) + cost[i];
}
// 最后一步可以是倒数第二级台阶直接登顶,所以求倒数的两层台阶哪一个花费最小
return Math.min(dp[cost.length - 2], dp[cost.length - 1]);
};
优化:滚动数组可以把空间复杂度压缩为 O(1)。
var minCostClimbingStairs = function (cost) {
const dp = [];
dp[0] = cost[0];
dp[1] = cost[1];
for (let i = 2; i < cost.length; i++) {
const sum = Math.min(dp[1], dp[0]) + cost[i];
dp[0] = dp[1], dp[1] = sum;
}
return Math.min(dp[1], dp[0]);
};
62. 不同路径
- 62. 不同路径
- 0608,mid,quick
- 动态规划
var uniquePaths = function (m, n) {
// dp[i][j]:机器人到达(i,j)时的方法总数
const dp = Array.from(new Array(m), () => new Array(n).fill(0));
dp[0][0] = 1;
for (let i = 0; i < m; i++) {
for (let j = 0; j < n; j++) {
if (!i && !j) continue; // (0,0)的情况已初始化为1
else if (!i) dp[i][j] = dp[i][j - 1]; //(0,x) 的情况只能向右走到达
else if (!j) dp[i][j] = dp[i - 1][j]; //(x,0) 的情况只能向下走到达
else dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; // (i,j) 的情况向右/向下走达到
}
}
return dp[m - 1][n - 1];
};
优化:用一维数组存储 dp
- 因为
(i, j)位置只涉及到上一个、左一个位置的值。所以用一维数组dp[]统计(i-1, j)即上一列的值,然后内层 for 循环一次,就遍历了一行坐标,dp 对应更新一次。
var uniquePaths = function (m, n) {
// 初始化时,全部赋值为1,边界的第一行(i,x)全部为1。
const dp = new Array(n).fill(1);
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
// 等式右边的 dp[j] 是上一行计算的结果,也就是 (i-1,j) 的总次数。
// 等式右边的 dp[j-1],是上一列计算的结果,也就是 (i, j-1) 的总次数。
dp[j] = dp[j] + dp[j - 1];
}
}
return dp[n - 1];
};
63. 不同路径 II
- 63. 不同路径 II
- 0608,mid,slow
- 动态规划
在初始化时,原本(上一题)一行一列都为 1,意为有一种方法到达该点。而在这道题中,如果最上边一行的中间有一个障碍物,则障碍物右边的所有位置都无法到达。
- 所以初始化时,默认所有位置值为 0。然后对第一行、第一列进行 for 循环遍历,赋值初始化为1,当遇到障碍物时截止。
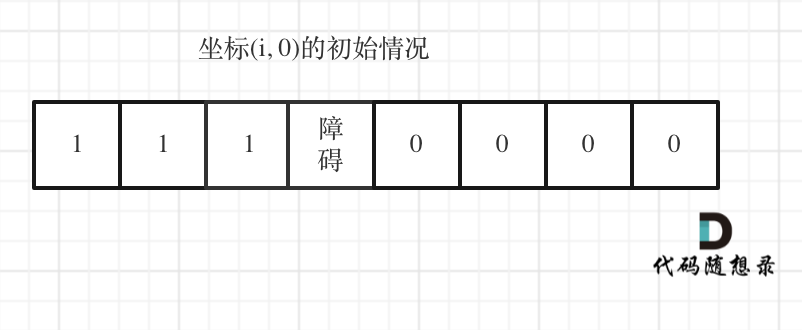
然后进行对 (i,j) 进行遍历,遇到障碍物就跳过(因为所有点已经初始化为0)。
- 理论上讲,如果当前点
(i, j)遇到上方有障碍物,只能通过左侧走到。dp[i][j] = dp[i-1][j],- 而实际上
(i-1, j)这个点已经初始化为0,所以不用特殊判断, - 全部用
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]即可。
- 而实际上
var uniquePathsWithObstacles = function (obstacleGrid) {
const m = obstacleGrid.length;
const n = obstacleGrid[0].length;
const dp = Array.from(new Array(m), () => new Array(n).fill(0));
// 初始化第一列(x, 0) 遇到障碍之前
for (let i = 0; i < m && obstacleGrid[i][0] === 0; i++) dp[i][0] = 1;
// 初始化第一行(0, x) 遇到障碍之前
for (let j = 0; j < n && obstacleGrid[0][j] === 0; j++) dp[0][j] = 1;
for (let i = 1; i < m; i++) {
for (let j = 1; j < n; j++) {
// 如果当前位置有障碍,就不能到达
if (obstacleGrid[i][j]) continue;
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[obstacleGrid.length - 1][obstacleGrid[0].length - 1];
};
343. 整数拆分
- 343. 整数拆分
- 0608,mid,answer
- 动态规划
【有点绕】
假定一个整数为 n,它被拆分后的最大乘积 k。则 n 和 k 的大小关系无法确定:
- 若 n 为 2,则拆分最大乘积为 1,小于自身;
- 若 n 为 10,则拆分最大乘积为 36,大于自身;
所以:
定义
dp[i]:表示整数 i 的拆分最大乘积。状态转移方程:
利用 for 循环,让
dp[i]一分为二,j + (i-j),遍历所有一分为二的情况,注意 j 的取值范围为[1, n-1]。- 情况一:求这两个数的乘积:
j * (i-j),把 i 拆分成两个数相乘; - 情况二:把
j换为最大乘积,也就是dp[j],把 i 拆分成两个以上的数相乘;- 为什么没有
j和j-i都拆分的情况? - 答:已经包含了:当
j-i为 1 的时候
- 为什么没有
- 情况一:求这两个数的乘积:
dp[i]最终的值就是 for 循环中所有的情况(每一个 j 对应的这两种情况)的最大值。

var integerBreak = function (n) {
// dp[i] 表示正整数i的最大乘积
const dp = [];
dp[2] = 1;
for (let i = 3; i <= n; i++) {
//把i拆分为:j + (i-j) 两个数。j的取值范围:2~j-1
let curMax = 0;
for (let j = 1; j < i - 1; j++) {
curMax = Math.max(curMax, j * (i - j), j * dp[i - j]);
}
dp[i] = curMax;
}
return dp[n];
};
96. 不同的二叉搜索树
- 96. 不同的二叉搜索树
- 0609,mid,answer
- 动态规划
构造二叉搜索树,重点不是这棵树的最大值,而是这棵树的元素总数。
- 换句话说,最大值为 n 时,可以构造出的二叉搜索树总数 === 元素为
[2, n+2]时可以构造出的二叉搜索树总数。重点是看总数量,是否从 0 开始则不是必须的。 - 随时复习:二叉搜索树的中序遍历结果是一个递增序列。
三种方法是依次递增的:
- 暴力递归、优化递归、最后总结出动态规划。
方法一:递归|暴力
思路:
第一步:求最大值为 n 时,可以构造出几种二叉搜索树
- 问题转化为元素有 n 个时,可以构造出几种二叉搜索树;
- 1~n 这几个结点,每个结点都有可能当作头结点;
- 如果 i 为头结点,则左子树的元素为:
[1, i-1],右子树的元素为:[i+1, n]; - 则 i 为头结点时构造出的总数 = 元素总数为
i-1时构造的二叉搜索树总数 * 元素总数为n - i时构造的二叉搜索树总数。 - 以此类推,把 1~n 全部的总数全部累加即可。
得出递归:
var numTrees = function (n) {
if (n <= 1) return 1;
let count = 0;
for (let i = 1; i <= n; i++) {
const leftNum = numTrees(i - 1);
const rightNum = numTrees(n - i);
count += leftNum * rightNum;
}
return count;
};
方法二:递归|优化
第二步:减少重复计算
上面的问题是,元素个数位 i 时可以构造的二叉搜索树总数,有可能会重复计算,需要剔除这些重复计算:
用 map 结构统计,按元素总数的不同分别记录:
var numTrees = function (n) {
const map = new Map();
map.set(0, 1); // 当元素总数为0时,为了方便做乘积运算,设置为1.
map.set(1, 1);
return getTrees(n);
function getTrees(n) {
if (map.has(n)) return map.get(n);
let count = 0;
for (let i = 1; i <= n; i++) {
const leftNum = getTrees(i - 1);
const rightNum = getTrees(n - i);
count += leftNum * rightNum;
}
map.set(n, count);
return count;
}
};
方法三:动态规划|总结
从上面的递归思路可以总结出结论:
把 map 结构转化为一个 array 结构。array 中成员下标就是对应 map 的 key,值就是对应 map 的 value,这个 array 其实是一个 dp:
设:dp[i] 表示元素总数为 i 时,可构造二叉搜索树的总个数。
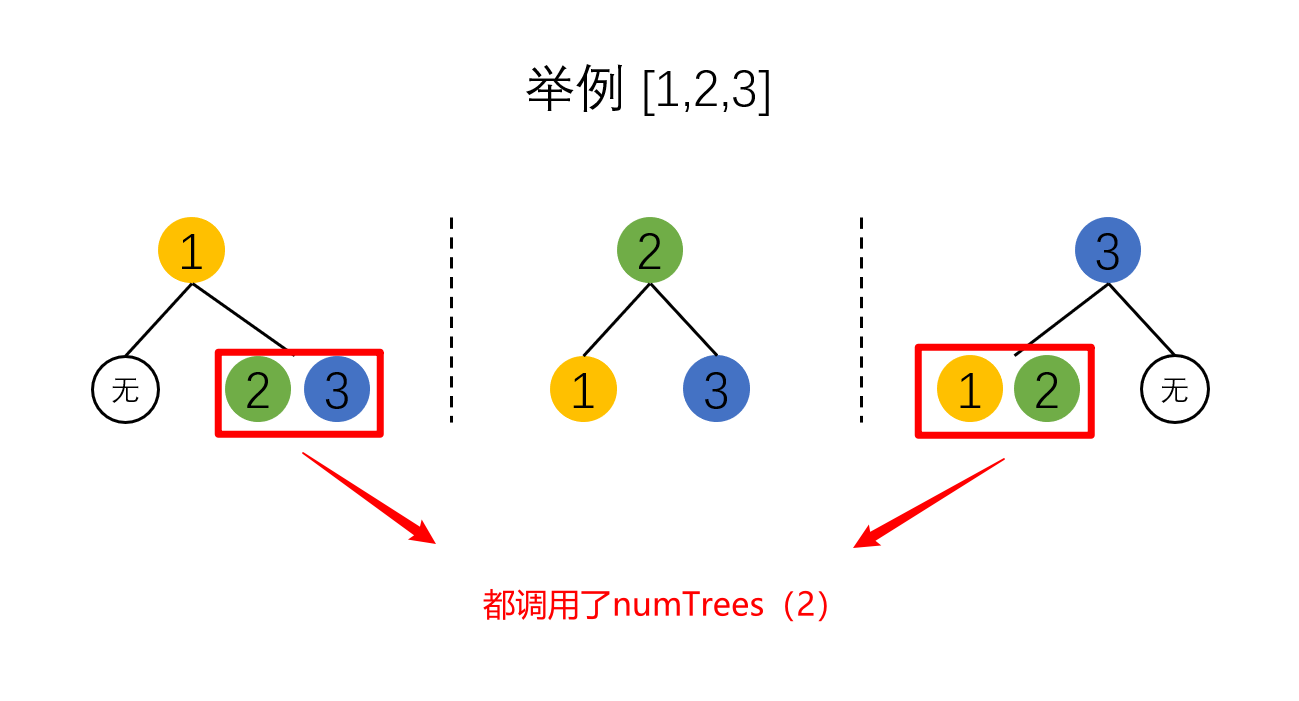
当元素总数为 3 时,分别有:
- 头结点为 1 时,左子树总数为 0,右子树总数为 2。可构造二叉搜索树的总个数为:dp[0] * dp[2]
- 头结点为 2 时,左子树总数为 1,右子树总数为 1。可构造二叉搜索树的总个数为:dp[1] * dp[1]
- 头结点为 3 时,左子树总数为 2,右子树总数为 0。可构造二叉搜索树的总个数为:dp[2] * dp[0]
最后:dp[3] = dp[0] * dp[2] + dp[1] * dp[1] + dp[2] * dp[0];
以此推广,当元素总数为 i 时,动态转移方程为:
- 遍历所有头结点的情况:头结点 j 的范围为
[1, i-1]。- 假设 i = 7,j = 3:则左侧元素个数为
j-1==> 2,右侧元素个数为i-j==> 4。
- 假设 i = 7,j = 3:则左侧元素个数为
dp[i] += dp[j-1] * dp[i-j]
for (let i = 2; i <=n; i++) { // 从2开始,0和1已经初始化为1
for (let j = 1; j <=i; j++) {
dp[i] += dp[j-1] * dp[i-j];
}
}
最后,得代码:
var numTrees = function (n) {
// 因为dp[i]在for循环重要做 += 运算,所以必须有一个初始值
const dp = new Array(n + 1).fill(0);
dp[0] = 1, dp[1] = 1;
for (let i = 2; i <= n; i++) {
for (let j = 1; j <= i; j++) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n]
};
0 1 背包问题
理解不了,就自己画一个二维数组模拟过程,然后执行代码的同时console.log一下过程。
作为「0-1 背包问题」,它的特点是:「每个数只能用一次」。解决的基本思路是:物品一个一个选,容量也一点一点增加去考虑,这一点是「动态规划」的思想,特别重要。
举例:🔍
背包最大重量为 4 。物品为:
| 重量 | 价值 | |
|---|---|---|
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少?
- 重量数组:
weight,其中weight[i]表示物品 i 的重量; - 价值数组:
value,其中value[i]物品 i 的价值。
二维dp数组
动态规划的 3 + 2 步:
- dp 数组的含义
dp[i][j] :从下标为 [0-i] 的物品里任意取 x 个,放进容量为 j 的背包,所得价值总和最大是多少。
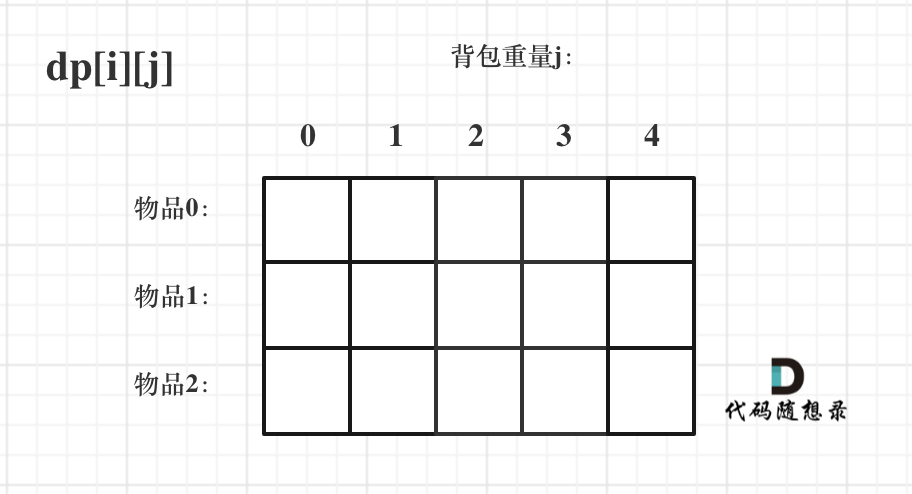
- 递推公式
从 dp[i-1][xxx] 系列中(也就是从 [1, i-1] 随便取的最大价值),有两个情况可以推出来 dp[i][j]:
- 不放物品 i:由
dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。- 当物品 i 的重量大于背包 j 的重量时,物品 i 无法放进背包中,所以被背包内的价值依然和前面相同。
- 放入物品 i:由
dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]]为背包容量为j - weight[i]的时候不放物品 i 的最大价值,那么dp[i - 1][j - weight[i]] + value[i](物品i的价值),就是背包放物品 i 得到的最大价值。
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
- 初始化 dp 数组
二维 dp 的初始化,主要在讨论上边 / 左边 两条边的情况:
- 当背包容量 j === 0 时,啥都放不下,所以
dp[x][0]应当都为 0; - 当物品 i === 0 时,只有一个物品可以讨论,当背包容量可以下 i 时,最大利润就是
value[0],放不下,最大利润是0;
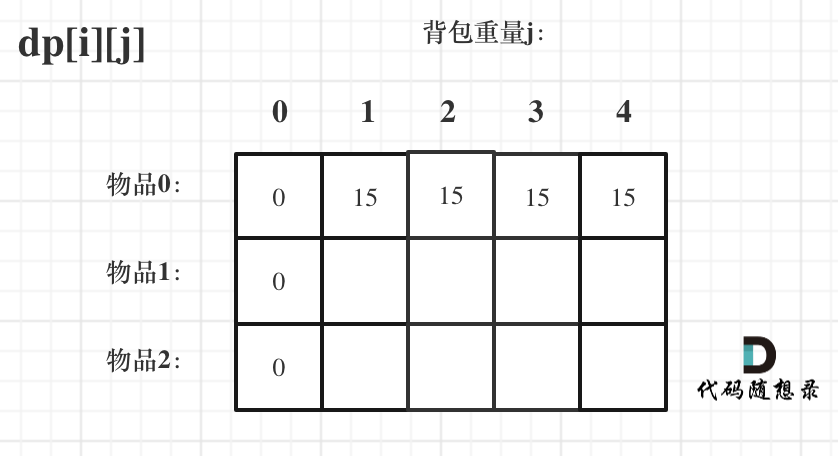
所以,初始化是把二维数组的所有成员都置为0,然后重置一下 dp[0][x] 最上方一行即可。
- 遍历顺序
for (let i = 1; i < weight.length; i++) { // 遍历物品
for (let j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 如果本身就放不下
else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
- 模拟推导
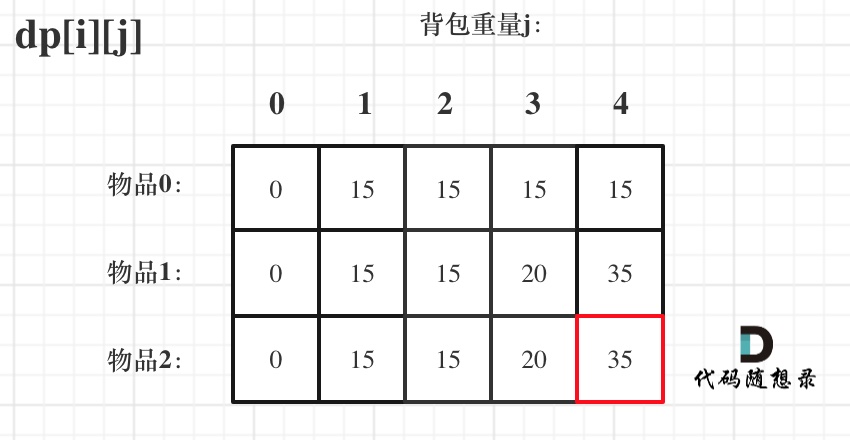
代码:
var weightbagproblem = function (weight, value, bagweight) {
// 定义dp
const dp = Array.from(new Array(weight.length), () => new Array(bagweight + 1).fill(0));
// 初始化 dp[0][x]
for (let j = weight[0]; j <= bagweight; j++)
dp[0][j] = value[0];
for (let i = 1; i < weight.length; i++) { // 遍历物品
for (let j = 0; j <= bagweight; j++) { // 遍历背包容量
if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 如果本身就放不下
else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
}
}
return dp[weight.length - 1][bagweight];
};
console.log(weightbagproblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
一维dp数组(滚动数组)
1. 定义 dp 数组
将二维数组转化为一维数组:dp[i][j] ====> dp[j]
2. 定义状态转移方程
上一题中,状态转移方程:
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
可以看到,dp[i][j] 是从 dp[i-1][x] 这一行得出的,在二维数组dp中,就是 dp[i][j] 的上一行。所以,当前判断的 dp 值,只依赖它上一行的一维 dp 数组。而其余的一维数组则没必要维护了。
修改后的状态转移方程:
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
但是需要注意的是,这里利用一维数组 dp[] 的反复写入,即新一行 dp[i][x] 的结果,会覆盖 dp[i-1][x] 的数据。所以要在写入时,要避免先覆盖掉后面还要用的值。比如 :
// 假如 weight(2) = 1
// 遍历某行 2:
dp[1] = Math.max(dp[1], dp[1 - weight[2]] + value[2]); // ==> Math.max(dp[1], dp[0] + value[2])
dp[2] = Math.max(dp[2], dp[2 - weight[2]] + value[2]); // ==> Math.max(dp[2], dp[1] + value[2])
...
3. 一维dp数组初始化
初始化放在了 for 循环遍历中,外层的 i 从 0 开始遍历。
唯一需要确定的是 dp[0] = 0。
4. 定义 for 遍历
这里可以看到,在求 dp[1] 时,用到了 dp[0] 的值;在求 dp[2] 时,用到了 dp[1] 的值:
也就是 dp[i] 数组中靠后的数,会用到在数组中它左边的 / 更靠前的值。那么我们在进行循环时,不能从左到右循环,提前覆盖掉会用的值,而是从右到左循环,先覆盖靠后的数。
同时,j 的遍历范围为 [weight[i], bagWeight]这里做了一个剪枝:
- 背包容量只有大于当前物品 i 的重量(weight[i])时,
dp[j]才有可能比之前有更大的值,否则背包放不下物品 i,dp[j]的值不会发生改变。- 这样子就省去了在两层 for 循环中,再添加一个 if 判断情况了。
- 同时也进行了 i == 0 时的 dp 初始化。
得到 for 循环:
for (let i = 0; i < weight.length; i++) { // 遍历物品
for (let j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
最后代码如下:
var weightbagproblem = function (weight, value, bagweight) {
// 定义dp
const dp = new Array(bagweight + 1).fill(0);
// i从0开始遍历,达到初始化 dp[0][x]
for (let i = 0; i < weight.length; i++) { // 遍历物品
for (let j = bagweight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
return dp[bagweight];
};
console.log(weightbagproblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
416. 分割等和子集
- 416. 分割等和子集
- 0609,mid,
- 动态规划、背包问题
方法一:背包|二维dp
0 1 背包问题:dp[i][j],表示随意选取在区间 [0, i] 内的物品,可以将容量为 j 的背包装满(或尽可能满)。
而这道题要求:随意选取在区间 [0, nums.length] 内的数字,可否等于 数组 nums 全部数字和的一半。
- 这里转化为 01 背包,需要考虑的点就是 “将数字分割相等的两个子集”,其实就是选取一些数,其和是 nums 总和的一半。
(1)定义二维 dp
dp[i][j] 表示选取区间 [0,i] 之间的数字,其总和是否刚好等于 j。等于为 true,不等于为 false。
(2)确定状态转移方程:
有2种情况:
- 不选择
nums[i]:如果[0, i-1]的选择区间内,已经有一部分元素的和为j,这里继续用同样的选择方案,自然也可以为 true。 - 选择
nums[i]:[0, i-1]的选择区间内,刚好有总和等于j - nums[i]的。如果dp[i-1][j - nums[i]] === true,那么dp[i][j]就相当于在dp[i-1][j - nums[i]]的基础上,多加一个新纳入可选择区间的nums[i],自然也为 true。
两种情况只要有一个为 true, dp[i][j] 就可以为 ture。
dp[i][j] = dp[i-1][j] 或者 dp[i-1][j- nums[i]]
但判断不选择时,要先判断 j- nums[i] 是否大于等于 0,如果小于 0 则不存在 dp[i-1][j- nums[i]]。如果等于 0 ,则刚好可以放下 nums[i],从这里可以看到下一步初始化的一些问题:
dp[x][0]应当等于 true。
(3)初始化 dp
初始化时,要考虑左边、上边的两条边界是否需要初始化。
dp[x][0]中,dp[x][0] = truedp[0][x]中,dp[0][nums[0]] = true
(4)for 循环
外层遍历 i:从 0 ~ nums.length - 1,是每次可选择的区间。
内层遍历 j:从 0 ~ nums 总和的一半。
得代码:
var canPartition = function (nums) {
// 如果长度为1,则直接false
if (nums.length <= 1) return false;
// 求数组总和的一半
let count = nums.reduce((prev, curv) => prev + curv);
// 如果总和不是2的倍数,无法平均分两半,则直接返回false
if (count % 2 !== 0) return false;
count = count / 2;
// dp[i][j] 表示选取区间[0,i]之间的数字,其总和是否刚好等于j
const dp = Array.from(new Array(nums.length), () => new Array(count).fill(false));
// 初始化:
dp[0][nums[0]] = true;
for (let i = 0; i < nums.length; i++)
dp[i][0] = true;
for (let i = 1; i < nums.length; i++) {
for (let j = 0; j <= count; j++) {
if (j - nums[i] < 0) dp[i][j] = dp[i - 1][j];
else dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]];
}
}
return dp[nums.length - 1][count];
};
方法二:背包|一维dp
背包问题是可以把二维 dp 优化为一维 dp 的:
定义:dp[j] 判断选取 当前区间 之间的数字,其总和是否刚好等于 j。
状态转移方程:
for (let i = 1; i < nums.length; i++) {
for (let j = count; j >= nums[i]; j++) { // j 从后往前遍历
dp[j] = dp[j - nums[i]];
}
}
最后的代码:
var canPartition = function (nums) {
// 如果长度为1,则直接false
if (nums.length <= 1) return false;
// 求数组总和的一半
let count = nums.reduce((prev, curv) => prev + curv);
// 如果总和不是2的倍数,无法平均分两半,则直接返回false
if (count % 2 !== 0) return false;
count = count / 2;
// dp[j] 表示选取区间[0,i]之间的数字,其总和是否刚好等于j
const dp = new Array(count).fill(false);
// 初始化:
dp[nums[0]] = true;
dp[0] = true;
for (let i = 1; i < nums.length; i++) {
for (let j = count; j >= nums[i]; j--) { // j 从后往前遍历
// 如果 dp[j] == ture,则不选择 nums[i] 的方案已经可以,直接跳过;
if (dp[j]) continue;
// 如果 dp[j] !== false,则看看选择 nums[i] 的方案是否可行
dp[j] = dp[j - nums[i]];
}
}
return dp[count];
};
1049. 最后一块石头的重量 II(待做)
- 1049. 最后一块石头的重量 II
- 不是top100题
- 🔍
494. 目标和
- 494. 目标和
- 0610,mid,answer
- 动态规划,背包问题
思路转化为背包问题
本题和 416 分割等和子集的转换思路相似。01背包问题是选或者不选,但本题必须选,是选+还是选-。先将本问题转换为01背包问题。
假设所有符号为 + 的元素和为 x,符号为 - 的元素和的绝对值是 y。
我们想要的 target = 正数和 - 负数和 = x - y;已知 x 与 y 的和就是数组所有元素的总和:x + y = sum。
所以:x - (sum - x) = target ===> x = (target + sum) / 2 。
得出转化:
也就是我们要从 nums 数组里选出几个数,令其和为 x。
于是转化成了求容量为 x 的 01 背包问题 => 要装满容量为 x 的背包,有几种方案。
(1)定义 dp
dp[i][j]:表示在 [0, i] 区间内任意选择,填满总和为 j 的背包,有几种方案。
直接压缩为一维 dp[j]。
(2)状态转移方程
两种情况:不选择 nums[i] + 选择 nums[i]
dp[j] = dp[j] + dp[j - num[i]]
(3)初始化
特例1:如果 target 都绝对值大于数组总和 sum,不可能实现,返回 0;
特例2:如果 target + sum 不是偶数,这导致 x 不是整数,无法实现,返回 0;
// 初始化
dp[0] = 1;
dp[nums[0]] = nums[0] === 0 ? 2 : 1;
不能初始化 dp[nums[i]] = 1,因为背包容量有 0 的情况,假设:nums = [0, 0],背包容量为 0;
则 dp[0][0] 为 2:
- 选择物品 0,则总容量为 0,满足要求;
- 不选择物品 0,则总容量为 0,也满足要求。
所以,当 nums[0] 为 0 时,dp[nums[0]] 也就是 dp[0],也就是为 2。
(4)遍历
for (let i = 1; i < nums.length; i++) {
for (let j = bagSize; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
得出代码:
- 优化初始化,只需要 dp[0] = 1,然后 for 循环从 0 开始遍历 i
var findTargetSumWays = function (nums, target) {
const sum = nums.reduce((prev, curv) => prev + curv);
// 特例
if (Math.abs(target) > sum) return 0;
if ((sum + target) % 2) return 0;
// 求 bagSize
const bagSize = (sum + target) / 2;
const dp = new Array(bagSize + 1).fill(0);
// 初始化
dp[0] = 1;
for (let i = 0; i < nums.length; i++) { // 从0开始,只初始化dp[0]=1
for (let j = bagSize; j >= nums[i]; j--) {
dp[j] += dp[j - nums[i]];
}
}
return dp[bagSize];
};
474.一和零(待做)
完全背包问题
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是,每种物品有无限件。
二维dp数组
一维dp数组(滚动数组)
整体思路与 0 1 背包相差不大,主要的区别在于遍历的时机:
首先在回顾一下01背包的核心代码
for(let i = 0; i < weight.length; i++) { // 遍历物品
for(let j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量,倒序
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]); // 不选择 + 选择
}
}
我们知道 0 1 背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以物品是从小到大去遍历,即:
dp[i-1][j]:表示从[0, i-1]中选择出容量为 j 的最大价值;dp[i][j]:表示从[0, i]中选择出容量为 j 的最大价值;- 在选择物品 i 时,可以选择 1 次、2次、3次 ...
dp[j - weight[i]]:从小开始遍历时,较大的数会复用刚更新的较小的数。科学的证明
以下是零钱兑换II 的推导,其原理是一样的,这个易懂:
// 第i种硬币的面值
v = coins[i]
// 不选 + 选1个 + 选2个 + ... + 选k个
dp[i][j] = dp[i-1][j] + dp[i-1][j-v] + dp[i-1][j-2v] + .... + dp[i-1][j-kv]);
dp[i][j-v] = dp[i-1][j-v] + dp[i-1][j-2v]+ dp[i-1][j-3v] + .... + dp[i-1][j-kv]);
// 因为 j-kv 必须大于零,所以 dp[i][j] 和 dp[i][j-v] 最后的k值是相同的,
// 由此:
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-v])

for(let i = 0; i < weight.length; i++) { // 遍历物品
for(let j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量,正序
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
同时,完全背包问题因为没有背包容量的限制,遍历物品和容量的顺序可以颠倒:
// 先遍历背包,再遍历物品
for(let j = 0; j <= bagWeight; j++) {
for(let i = 0; i < weight.length; i++) {
// 判断:容量必须大于新增物品的重量,否则是不选择情况,容量不会变化。
if (j >= weight[i]) dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i])
}
}
最终得出代码:
// 先遍历物品,再遍历背包容量
function test_completePack(weight, value, bagWeight) {
let dp = new Array(bagWeight + 1).fill(0)
for(let i = 0; i <= weight.length; i++) {
for(let j = weight[i]; j <= bagWeight; j++) {
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i])
}
}
console.log(dp)
}
test_completePack([1, 3, 5], [15, 20, 30], 4)
322. 零钱兑换
- 322. 零钱兑换
- 0610,mid,answer
- 动态规划,完全背包
方法一:二维dp
这里代码还有点小问题,更多细节看 这里,完全背包问题通常不会使用二维数组去解决。因为相比 01 背包,完全背包不限制选择的次数,状态转移方程中在判断 “选择” 时,需要额外的一个 for 循环去挨个分析:选择1个、选择2个、....。
但是,如果使用一维 dp 数组,则多次选择的问题,在 for 背包容量从小到大遍历时,就顺带全部计算在内了。
- 结论:完全背包问题直接用一维 dp 数组解决。
var coinChange = function (coins, amount) {
// f[i][j] 代表从[0, 1]随意选取coin,当总额是 j 时的最少硬币数
// 初始化为 Infinity,表示不满足情况时,值为 Infinity,方便参与计算。如果设置为-1,Math.min()的结果就永远为-1了
const dp = Array.from(new Array(coins.length), () => new Array(amount + 1).fill(Infinity));
// dp[0][x]: coin可选择为0时,只有总额为0时最少硬币数为0,除此之外都不构成组合,值为Infinity
dp[0][0] = 0;
// dp[x][0]: 总额为0时,coin不论什么区间最少硬币数都为0
for (let i = 0; i < coins.length; i++) dp[i][0] = 0;
for (let i = 1; i < coins.length; i++) {
for (let j = 0; j <= amount; j++) {
// 不选择新硬币的情况
dp[i][j] = dp[i - 1][j];
// 选择新硬币的情况,因为可以无限次数选择,那么需要一个for循环:选择1个、2个 ...直到不能再选择这么多
for (let k = 1; k * coins[i] <= j; k++) {
if (dp[i - 1][j - k * coins[i]] !== Infinity) {
dp[i][j] = Math.min(dp[i][j], dp[i - 1][j - k *coins[i]] + k);
}
}
}
}
console.log(dp);
return dp[coins.length - 1][amount] == Infinity ? -1 : dp[coins.length - 1][amount];
};
方法二:一维dp(正解)
一维数组才是此题正解
var coinChange = function (coins, amount) {
// dp[i] 代表当总额是 i 时的最少硬币数。
const dp = new Array(amount + 1).fill(Infinity);
dp[0] = 0;
for (let i = 0; i < coins.length; i++) {
for (let j = coins[i]; j <= amount; j++) {
dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
}
}
return dp[amount] == Infinity ? -1 : dp[amount];
};
518. 零钱兑换 II
- 518. 零钱兑换 II
- 0610,mid,answer
- 动态规划,完全背包
- 注意状态转移方程:
不选择和选择,都是面额为 j 的组合,所以两种情况都有效,加起来。
dp[j] = dp[j] + dp[j - coins[i]];
// 面额为j的总组合数 = 不选择物品i的总数 + 选择物品i的总数
二维维度:

一维维度:
在二维解法的基础上,直接取消「物品维度」;
确保「容量维度」的遍历顺序为「从小到大」(适用于「完全背包」);
将形如
f[i - 1][j - k * coin[i]]的式子更替为f[j − coin[i]],同时解决「数组越界」问题(将物品维度的遍历修改为从coin[i]开始)。注意遍历的顺序:
纯完全背包求的是能否凑成一个总和,或者让总和尽可能大。 不考虑凑成总和的元素是否存在特定顺序,有顺序也行,没有顺序也行。
而本题要求凑成总和的 组合数,元素之间是存在顺序问题的:{1, 3} 和 {3, 1} 一个相同的 组合方案,不同的 排列方案。
所以纯完全背包是能凑成总和就行,不用管怎么凑的。本题是求凑出来的方案总数,且每个方案总数就是组合数。
- 外层 for 循环遍历物品,内层 for 遍历背包:得出的是 组合方案;
- 外层 for 循环遍历背包,内层 for 遍历物品:得出的是 排列方案;
得出代码:
var change = function (amount, coins) {
// dp[i][j]: [0, i]区间内选择,面额正好等于j的组合总数.
const dp = new Array(amount + 1).fill(0);
dp[0] = 1;
for (let i = 0; i < coins.length; i++) { // 遍历物品
for (let j = coins[i]; j <= amount; j++) { // 遍历背包
dp[j] = dp[j] + dp[j - coins[i]];
}
}
return dp[amount];
};
377. 组合总和 Ⅳ
- 377. 组合总和 Ⅳ
- 0610,mid,answer
- 动态规划,背包问题
题目中要求,顺序不同的序列被视作不同的组合。所以,这里要改变 for 循环的嵌套关系:
如果是完全背包,数组中的元素可重复使用。同时,关注结果的顺序({1, 3} 和 {3, 1} 两个不同的 排列方案)
外层 for 遍历 nums (背包),内层 for 遍历 target (物品),且内循环正序 (重复拿):
代码如下:
var combinationSum4 = function (nums, target) {
// dp[i][j] 从区间[0,i]之间选择数,总和为j的组合种类
const dp = new Array(target + 1).fill(0);
dp[0] = 1;
for (let i = 0; i <= target; i++) { // 遍历背包
for (let j = 0; j < nums.length; j++) { // 遍历物品
if (i < nums[j]) continue;
dp[i] += dp[i - nums[j]];
}
}
return dp[target];
};
279. 完全平方数
- 279. 完全平方数
- 0610,mid,normal
- 动态规划,背包问题
犯错:初始化问题。
可以想到,在状态转移方程中求 Math.min(),所以各值初始化应当为 Infinity,如果设置为 0(我就是这样犯错了),那一定永远无法被更新,0 一直是最小的。
同时 dp[0] = [0] 是为了满足可以完成题解,没有任何实际意义,n 是从 1开始统计的。如果 dp[0] 设置为 Infinity,无法正确出结果。
var numSquares = function (n) {
// 完全背包 + 无顺序组合
// dp[i][j], 从[0, i]中选择数字,和为j的最少数量
const dp = new Array(n + 1).fill(Infinity);
dp[0] = 0;
for (let i = 0; i <= n; i++) {
for (let j = i ** 2; j <= n; j++) {
// 选择,不选择
dp[j] = Math.min(dp[j], dp[j - i ** 2] + 1);
}
}
return dp[n]
};
139. 单词拆分
- 139. 单词拆分
- 0611,mid,quick
本题有三个不同点:
(1)dp 的定义
dp[i][j] 为从 wordDict 中选择 [0, i] 范围内的单词,是否可以拼出 s 字符串前 j 个元素。
- 所以,在定义 dp 时,长度为
s.length + 1,如 s ='leetcode',dp 长度为 9,dp[8]表示 'leetcode';dp[1]表示'l'。 - 而
dp[0]没有任何意义,只提供一个初始的 ture。对 j 的遍历 从 1 开始即可。
(2)for 循环是否要求顺序
回顾之前的总结:
如果要求组合,则结果无顺序,遍历要先物品再背包,其特点
- 物品 i 在外层,从头至尾只遍历一次,所以物品的选择只有 {1, 5} 这样,不会出现 {5, 1},也就排除了顺序不同的重复结果。
如果要求排列,则结果有顺序,遍历要先背包再物品,其特点
- 物品 j 在内层,所以每当容量 j 发生一次变化,物品都要从
[0, i]再遍历一边,会出现 {1, 5} 和 {5, 1} 这样顺序不同的结果。
- 物品 j 在内层,所以每当容量 j 发生一次变化,物品都要从
而本题的第 2 个例子:
输入: s = "applepenapple", wordDict = ["apple", "pen"]
输出: true
解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
可以看到,'apple' 作为 i == 0 的物品,在开头用过一次,末尾也用过一次。所以本题需要反复遍历物品结果,则选择 ‘要求顺序’。
如果对此理解不透彻,可以把两种顺序调换一下,打印一下内存 for 循环的 log,就能看出来区别。
(3)状态转移方程
本题是字符串,所以物品 i 的遍历是对 wordDict 数组遍历,一组单词整体判断。而容量 j 依然是一个字母一个字母的添加。
if (j < wordDict[i].length) continue;
- 如果当前容量 j 小于新加入的单词长度,则
[0, j]区间的字符串一定没有新单词的加入,所以dp[j]不做修改,之前能拼成(true),就继续为 true;不能拼成(false),就继续为 false。
if (!dp[j] && wordDict[i] === s.substring(j - wordDict[i].length, j)) {
dp[j] = dp[j - wordDict[i].length];
}
如果 dp[j] 之前为 true,那现在一定也为 true,不用判断这个字符串。
当 !dp[j] 时,需要判断:如果在 [0, wordDict[i]] 区间的有某个单词(物品),刚好等于容量 j 的最后几个单词,比如:
s 为
leetcode,当 i== 2,j = 8, 时(从1计算):s.substring(j - wordDict[i].length, j)
==> s.substring(8 - 4, 8)
==> s.substring(4, 8)
==> 'code' // 刚好等于 wordDict[i]
// 此时,
dp[j] = dp[j - wordDict[i].length]
==> = dp[8 - 4] ==> dp[4]
// 然后 dp[5] 之间已经计算过,其 leet 刚好在 wordDict 中有对应单词,dp[4] = dp[4 - 4] 为 dp[0],其值曾初始化为 true。
// 自然, dp[0]、dp[4]、dp[8] 都为 true
得代码:
var wordBreak = function (s, wordDict) {
// dp[i][j] 从dict中前[0,i]个单词中选择,能否拼出来[0,j]区间的s字符串
const dp = new Array(s.length + 1).fill(false);
dp[0] = true;
for (let j = 1; j <= s.length; j++) {
for (let i = 0; i < wordDict.length; i++) {
// 不选择(不能选择)
if (j < wordDict[i].length) continue;
// 不选择 + 选择
// console.log(j, wordDict[i], s.substring(j - wordDict[i].length, j));
if (!dp[j] && wordDict[i] === s.substring(j - wordDict[i].length, j)) {
dp[j] = dp[j - wordDict[i].length];
}
}
}
// console.log('end', dp);
return dp[s.length];
};
背包问题总结:
常见的背包问题有:
- 组合问题:
- True、False 问题:
- 最大最小问题:
看到问题后,需要做到以下几个步骤:
- (背包问题):分析是否为背包问题。
- (哪种背包):是 0-1 背包问题,还是完全背包问题,也就是题目给的 nums 数组中的元素是否可以重复使用。
- (状态方程):判定是 组合问题、True、False问题、最大最小问题哪一种。
- (遍历顺序):如果是组合问题,是否需要考虑元素之间的顺序,这影响到 for 遍历物品和背包的顺序。
(1)状态转移方程
组合问题公式
dp[i] = dp[i] + dp[i-num];
True、False 问题公式
dp[i] = dp[i] or dp[i-num];
最大最小问题公式
dp[i] = Math.min(dp[i], dp[i-num]+1);
// 或者
dp[i] = Math.max(dp[i], dp[i-num]+1);
(2 + 3)是否为背包问题
背包问题具备的特征:
- 一个 target,target 可以是数字也可以是字符串,这个是 背包容量
- 一个数组 nums,nums 中装的可能是数字,也可能是字符串,这个是 全部物品
问:能否使用 nums 中的元素做各种排列组合得到 target?
nums 中的数字只能使用一次:0 1 背包
nums 中的数字可以使用 n 次:完全背包
(4)确定遍历顺序
如果是组合问题,需要确定 for 循环遍历的顺序:
如果是 0 1 背包,数组中的元素不可重复使用。
外层 for 遍历 nums (物品),内层 for 遍历 target (背包),且内循环倒序 (不可重复拿):
for (let i = 0; i < nums.length; i++) { // 遍历物品
for (let j = target; j >= nums[i]; j--) { // 遍历背包容量,倒序
dp[j] = Math.max(dp[j], dp[j - nums[i]] + value[i]);
}
}如果是完全背包,数组中的元素可重复使用。同时,不关注结果的顺序({1, 3} 和 {3, 1} 一个相同的 组合方案)
外层 for 遍历 nums (物品),内层 for 遍历 target (背包),且内循环正序 (重复拿):
for (let i = 0; i < nums.length; i++) { // 遍历物品
for (let j = nums[i]; j <= target; j++) { // 遍历背包,正序
dp[j] += dp[j - nums[i]];
}
}如果是完全背包,数组中的元素可重复使用。同时,关注结果的顺序({1, 3} 和 {3, 1} 两个不同的 排列方案)
外层 for 遍历 nums (背包),内层 for 遍历 target (物品),且内循环正序 (重复拿):
for (let i = 0; i < nums.length; i++) { // 遍历物品
for (let j = nums[i]; j <= target; j++) { // 遍历背包
dp[j] += dp[j - nums[i]];
}
}